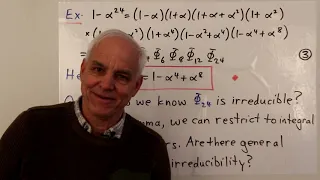Orthogonal polynomials | Special hypergeometric functions
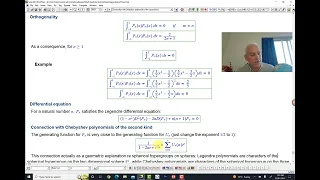
In mathematics, Gegenbauer polynomials or ultraspherical polynomials C(α)n(x) are orthogonal polynomials on the interval [−1,1] with respect to the weight function (1 − x2)α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials. They are named after Leopold Gegenbauer. (Wikipedia).
Advice for research maths | The joy of maxel number theory and Gegenbauer polynomials | Wild Egg
We extend our Legendre polynomial maxel approach to the larger more general situation of Gegenbauer polynomials and their maxels. Now these depend on a parameter r, which is directly related to the dimension of the corresponding sphere on which the hypergroup structure gives characters whi
From playlist Maxel inverses and orthogonal polynomials (non-Members)
Advice for Research Maths | Properties of Legendre and Gegenbauer polynomials | Wild Egg Maths
To try to understand how to apply two dimensional maxel magic to the family of Legendre polynomials, let's look at some properties of these polynumbers, including differential equations, connections with Chebyshev polynomials, and how they arise from the geometry of the sphere and an assoc
From playlist Maxel inverses and orthogonal polynomials (non-Members)
Advice Maths Research | The Jacobi polynumber maxel challenge! | Wild Egg Maths
We introduce the Jacobi polynomials which are extensions, in some sense, of the Gegenbauer polynomials and play a major role in representation theory. In this talk we outline explorations that you can make, following the two-dimensional maxel approach to number theory and orthogonal polyno
From playlist Maxel inverses and orthogonal polynomials (non-Members)
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems
Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
matrix choose a matrix. Calculating the number of matrix combinations of a matrix, using techniques from linear algebra like diagonalization, eigenvalues, eigenvectors. Special appearance by simultaneous diagonalizability and commuting matrices. In the end, I mention the general case using
From playlist Eigenvalues
Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
What We've Learned from NKS Chapter 10: Processes of Perception and Analysis
In this episode of "What We've Learned from NKS", Stephen Wolfram is counting down to the 20th anniversary of A New Kind of Science with [another] chapter retrospective. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or th
From playlist Science and Research Livestreams
Linear Algebra: Ch 3 - Eigenvalues and Eigenvectors (5 of 35) What is an Eigenvector?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain and show (in general) what is and how to find an eigenvector. Next video in this series can be seen at: https://youtu.be/SGJHiuRb4_s
From playlist LINEAR ALGEBRA 3: EIGENVALUES AND EIGENVECTORS
What is the multiplicity of a zero?
👉 Learn about zeros and multiplicity. The zeroes of a polynomial expression are the values of x for which the graph of the function crosses the x-axis. They are the values of the variable for which the polynomial equals 0. The multiplicity of a zero of a polynomial expression is the number
From playlist Zeros and Multiplicity of Polynomials | Learn About
On the symmetries of and equivalence test for design polynomials by Nikhil Gupta
Discussion Meeting Workshop on Algebraic Complexity Theory  ORGANIZERS Prahladh Harsha, Ramprasad Saptharishi and Srikanth Srinivasan DATE & TIME 25 March 2019 to 29 March 2019 VENUE Madhava Lecture Hall, ICTS Bangalore Algebraic complexity aims at understanding the computationa
From playlist Workshop on Algebraic Complexity Theory 2019
Superpolynomial Lower Bounds Against Low-Depth Algebraic Circuits I... - Srikanth Srinivasan
Computer Science/Discrete Mathematics Seminar I Topic: Superpolynomial Lower Bounds Against Low-Depth Algebraic Circuits I : An overview Speaker: Srikanth Srinivasan Affiliation: Aarhus University Date: September 27, 2021 Every multivariate polynomial P(x_1,...,x_n) can be written as a
From playlist Mathematics
Linear Algebra 2i: Polynomials Are Vectors, Too!
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Part 1 Linear Algebra: An In-Depth Introduction with a Focus on Applications
Francesco Mezzadri: Moments of Random Matrices and Hypergeometric Orthogonal Polynomials
We establish a new connection between moments of n×n random matrices $X_{n}$ and hypergeometric orthogonal polynomials. Specifically, we consider moments $\mathbb{E}\mathrm{Tr} X_n^{-s}$ as a function of the complex variable $s\in\mathbb{C}$, whose analytic structure we describe completely
From playlist Jean-Morlet Chair - Grava/Bufetov
Proof of the existence of the minimal polynomial. Every polynomial that annihilates an operator is a polynomial multiple of the minimal polynomial of the operator. The eigenvalues of an operator are precisely the zeros of the minimal polynomial of the operator.
From playlist Linear Algebra Done Right
In this video I discuss irreducible polynomials and tests for irreducibility. Note that this video is intended for students in abstract algebra and is not appropriate for high-school or early college level algebra courses.
From playlist Abstract Algebra
How to reorder and classify a polynomial based on it's degree and number of terms
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations