
How to find all of the solutions to an equation as well as within the unit circle
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric identities, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the give
From playlist Solve Trigonometric Equations

Find all the solutions of trig equation with cotangent
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given
From playlist Solve Trigonometric Equations

How to find all the solutions to a trigonometric equation
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Taking the Square Root

Solving a trigonometric equation with cosine equal to negative one
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric identities, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the give
From playlist Solve Trigonometric Equations

Lecture 24 (CEM) -- Introduction to Variational Methods
This lecture introduces to the student to variational methods including finite element method, method of moments, boundary element method, and spectral domain method. It describes the Galerkin method for transforming a linear equation into matrix form as well as populating the global matr
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering
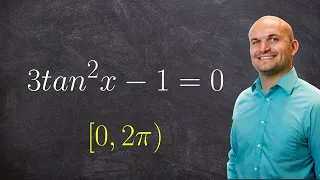
How to solve trigonometric equation with tangent
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Taking the Square Root

Promoting global stability in data-driven models of quadratic nonlinear dynamics - Trapping SINDy
System identification methods attempt to discover physical models directly from a dataset of measurements, but often there are no guarantees that the resulting models are stable. This video abstract summarizes our recent work that builds in a notion of long-term boundedness (or global stab
From playlist Research Abstracts from Brunton Lab

Rigorous analysis and numerical implementation... - Titi - Workshop 2 - CEB T3 2019
Titi (Texas A&M U, USA) / 14.11.2019 Rigorous analysis and numerical implementation of a data assimilation algorithm ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriP
From playlist 2019 - T3 - The Mathematics of Climate and the Environment

Solving a trigonometric equation by taking the square root of both sides
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Taking the Square Root

Ari Stern: Hybrid finite element methods preserving local symmetries and conservation laws
Abstract: Many PDEs arising in physical systems have symmetries and conservation laws that are local in space. However, classical finite element methods are described in terms of spaces of global functions, so it is difficult even to make sense of such local properties. In this talk, I wil
From playlist Numerical Analysis and Scientific Computing

Machine Learning for Computational Fluid Dynamics
Machine learning is rapidly becoming a core technology for scientific computing, with numerous opportunities to advance the field of computational fluid dynamics. This paper highlights some of the areas of highest potential impact, including to accelerate direct numerical simulations, to i
From playlist Data Driven Fluid Dynamics

Lec 17 | MIT 18.085 Computational Science and Engineering I, Fall 2008
Lecture 17: Finite elements in 1D (part 1) License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.085 Computational Science & Engineering I, Fall 2008

Solving a trig function with sine and cosine
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Factoring

Valeria Simoncini: Computational methods for large-scale matrix equations and application to PDEs
Linear matrix equations such as the Lyapunov and Sylvester equations and their generalizations have classically played an important role in the analysis of dynamical systems, in control theory and in eigenvalue computation. More recently, matrix equations have emerged as a natural linear a
From playlist Numerical Analysis and Scientific Computing

Thermalisation, Many-Body Chaos, and Weak Solutions.. by Samriddhi Sankar Ray
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Numerical relativity: Computational methods by Harald Pfeiffer
PROGRAM : GRAVITATIONAL WAVE ASTROPHYSICS (ONLINE) ORGANIZERS : Parameswaran Ajith, K. G. Arun, Sukanta Bose, Bala R. Iyer, Resmi Lekshmi and B Sathyaprakash DATE : 18 May 2020 to 22 May 2020 VENUE : ONLINE Meeting Due to the ongoing COVID-19 pandemic, the original program has been canc
From playlist Gravitational Wave Astrophysics (Online) 2020

How to find all of the solutions of an equation with secant
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric identities, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the give
From playlist Solve Trigonometric Equations
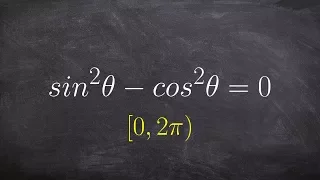
Solving a trigonometric equation with applying pythagorean identity
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Factoring

Rec 8 | MIT 18.085 Computational Science and Engineering I, Fall 2008
Recitation 8 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.085 Computational Science & Engineering I, Fall 2008

How to write all the solutions to a trig equation that is squared
👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given eq
From playlist Solve Trigonometric Equations by Taking the Square Root