
C73 Introducing the theorem of Frobenius
The theorem of Frobenius allows us to calculate a solution around a regular singular point.
From playlist Differential Equations

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

The Frobenius Problem - Proof of the Formula for the Frobenius Number for Two Numbers
Describes how to derive the general formula for the Frobenius Number of two Numbers. Proves why Frob(m,n) = mn - m - n.
From playlist Proofs

The Frobenius Problem - Method for Finding the Frobenius Number of Two Numbers
Goes over how to find the Frobenius Number of two Numbers.
From playlist ℕumber Theory

The Frobenius Problem - Problem Statement
Describes the Frobenius Problem and goes over some trivial cases
From playlist ℕumber Theory

Russell's Paradox - A Ripple in the Foundations of Mathematics
Bertrand Russell's set theory paradox on the foundations of mathematics, axiomatic set theory and the laws of logic. A celebration of Gottlob Frege. Thank you to Professor Joel David Hamkins for your help with this video. Hi! I'm Jade. Subscribe to Up and Atom for physics, math and com
From playlist Math
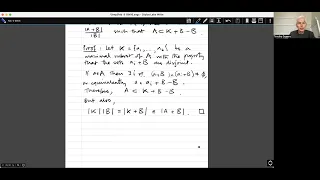
Introduction to additive combinatorics lecture 9.5 --- Freiman's theorem for subsets of F_p^N.
Freiman's theorem for subsets of F_p^N states that if A is a subset of F_p^N and |A + A| is at most C|A|, then there is a subspace X of F_p^N of size at most C'|A| that contains A, where C' depends only on C. The result is actually due to Imre Ruzsa. Here I give not Ruzsa's original proof,
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

The Road to Gödel's Incompleteness Theorems - Juliette Kennedy
Friends Lunch with a Member Topic: The Road to Gödel's Incompleteness Theorems Speaker: Juliette Kennedy Date: November 22, 2019
From playlist Friends of the Institute

Crisis in the Foundation of Mathematics | Infinite Series
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi What if the foundation that all of mathematics is built upon isn't as firm as we thought it was? Note: The natural numbers sometimes include zero and sometimes don't -
From playlist An Infinite Playlist

Most Famous Ethical Puzzle: The Frege-Geach Problem - Philosophy Tube
One of the most famous and difficult problems in ethics! The issue that killed moral noncognitivism – The Frege-Geach Problem! Ethics Playlist: https://www.youtube.com/playlist?list=PLvoAL-KSZ32ecfEjoNjMJyKTFUS5-hNr9 Subscribe! http://www.youtube.com/subscription_center?add_user=thephilos
From playlist A-Level Philosophy

The Frenet Serret equations (example) | Differential Geometry 19 | NJ Wildberger
Following from the last lecture on the Frenet Serret equations, we here look in detail at an important illustrative example--that of a helix. The Fundamental theorem of curves is stated--that the curvature and torsion essentially determine a 3D curve up to congruence. We introduce the osc
From playlist Differential Geometry

1.11.9 Russell's Paradox: Video
MIT 6.042J Mathematics for Computer Science, Spring 2015 View the complete course: http://ocw.mit.edu/6-042JS15 Instructor: Albert R. Meyer License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.042J Mathematics for Computer Science, Spring 2015

Automatizability and Simple Stochastic Games - Toniann Pitassi
Automatizability and Simple Stochastic Games Toniann Pitassi University of Toronto February 15, 2011 The complexity of simple stochastic games (SSGs) has been open since they were defined by Condon in 1992. Such a game is played by two players, Min and Max, on a graph consisting of max nod
From playlist Mathematics

The Frobenius Norm for Matrices
This video describes the Frobenius norm for matrices as related to the singular value decomposition (SVD). These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz Amazon: https://www.amazon.com/Da
From playlist Data-Driven Science and Engineering

How Do Names Work? Part II - Philosophy Tube
An examination of the referential theory of names, with some philosophy and linguistics. Knowledge, Logic, and Religion Playlist: https://www.youtube.com/playlist?list=PLvoAL-KSZ32fRrlUcuezyvR80Ec6qHUz_ Facebook: https://www.facebook.com/PhilosophyTube?ref=hl Twitter: https://twitter.com
From playlist KNOWLEDGE, LOGIC, & RELIGION

Set Theory - Russell's Paradox: Oxford Mathematics 3rd Year Student Lecture
This is the second of four lectures from Robin Knight's 3rd Year Set Theory course. Robin writes: "Infinity baffled mathematicians, and everyone else, for thousands of years. But around 1870, Georg Cantor worked out how to study infinity in a way that made sense, and created set theory. M
From playlist Oxford Mathematics Student Lectures - Set Theory

The Nature of Philosophy & Mathematics (Michael Dummett)
Michael Dummett discusses the nature of philosophy and mathematics and their a priori character in this clip from the beginning of a talk he gave on the philosophy of mathematics and Frege in 1994. The talk can be found here: https://youtu.be/ucPhfzCvKnE #Philosophy #Epistemology #Mathema
From playlist Shorter Clips & Videos - Philosophy Overdose

Differential Equations | Frobenius' Method part 2
From Garden of the Gods in Colorado Springs, we present a Theorem regarding Frobenius Series solutions to a certain family of second order homogeneous differential equations. An example is also explored. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Series Solutions for Differential Equations

Topology Without Tears - Video 2b - Infinite Set Theory
This is part (b) of Video 2, the second in a series of videos supplementing the online book "Topology Without Tears" which is available at no cost from www.topologywithouttears.net
From playlist Topology Without Tears

Differential Equations | Application of Abel's Theorem Example 2
We give an example of applying Abel's Theorem to construct a second solution to a differential equation given one solution. www.michael-penn.net
From playlist Differential Equations