
Infinite Limits With Equal Exponents (Calculus)
#Calculus #Math #Engineering #tiktok #NicholasGKK #shorts
From playlist Calculus

Applications of double integrals: examples
Free ebook http://tinyurl.com/EngMathYT Example of how to apply double integrals to compute mass and moments of thin plates.
From playlist Engineering Mathematics

Epsilon delta limit (Example 3): Infinite limit at a point
This is the continuation of the epsilon-delta series! You can find Examples 1 and 2 on blackpenredpen's channel. Here I use an epsilon-delta argument to calculate an infinite limit, and at the same time I'm showing you how to calculate a right-hand-side limit. Enjoy!
From playlist Calculus

FEM@LLNL | Unifying the Analysis of Geometric Decomposition in FEEC
Sponsored by the MFEM project, the FEM@LLNL Seminar Series focuses on finite element research and applications talks of interest to the MFEM community. On March 22, 2022, Tobin Isaac of Georgia Tech presented "Unifying the Analysis of Geometric Decomposition in FEEC." Two operations take
From playlist FEM@LLNL Seminar Series

An introduction to the double integral. Whereas the single integral determines the area under a curve, the double integral of a two variable function determines the volume under a surface as marked out by a region on the XY plane.
From playlist Advanced Calculus / Multivariable Calculus

DSI | Diagrammatic Differential Equations in Physics Modeling and Simulation
Abstract: I’ll discuss some results from a recent paper on applying categories of diagrams for specifying multiphysics models for PDE-based simulations. We developed a graphical formalism inspired by the graphical approach to physics pioneered by the late Enzo Tonti. We will discuss the gr
From playlist DSI Virtual Seminar Series

Download the free PDF http://tinyurl.com/EngMathYT A tutorial on the basics of setting up and evaluating double integrals. We show how to sketch regions of integration, their description, and how to reverse the order of integration.
From playlist Several Variable Calculus / Vector Calculus

Lecture 9: Discrete Exterior Calculus (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Ari Stern: Hybrid finite element methods preserving local symmetries and conservation laws
Abstract: Many PDEs arising in physical systems have symmetries and conservation laws that are local in space. However, classical finite element methods are described in terms of spaces of global functions, so it is difficult even to make sense of such local properties. In this talk, I wil
From playlist Numerical Analysis and Scientific Computing

Lecture 3: Exterior Algebra (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Lecture 8: Discrete Differential Forms (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858
Branimir Cacic, Classical gauge theory on quantum principalbundles
Noncommutative Geometry Seminar (Europe), 20 October 2021
From playlist Global Noncommutative Geometry Seminar (Europe)
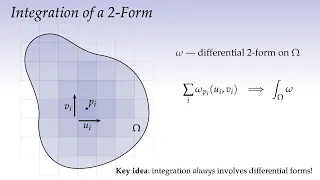
Lecture 7: Integration (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Masoud Khalkhali: Curvature of the determinant line bundle for noncommutative tori
I shall first survey recent progress in understanding differential and conformal geometry of curved noncommutative tori. This is based on work of Connes-Tretkoff, Connes-Moscovici, and Fathizadeh and myself. Among other results I shall recall the computation of spectral invariants, includi
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Calculus: Absolute Maximum and Minimum Values
In this video, we discuss how to find the absolute maximum and minimum values of a function on a closed interval.
From playlist Calculus

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions

Quantum Finite Elements: Lattice Field Theory on Curved Manifolds by Richard Brower
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

14_9 The Volume between Two Functions
Calculating the volume of a shape using the double integral. In this example problem a part of the volume is below the XY plane.
From playlist Advanced Calculus / Multivariable Calculus

