
What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions
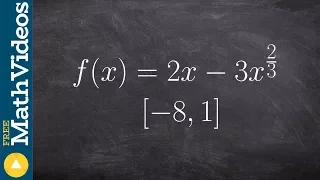
How to find the extrema using the EVT
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Determine the extrema of a function on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Determine the extrema using EVT of a rational function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Determine the extrema using the end points of a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Prove or Disprove if the Function is Injective
Prove or Disprove if the Function is Injective If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Functions, Sets, and Relations

Calculus - The Fundamental Theorem, Part 5
The Fundamental Theorem of Calculus. How an understanding of an incremental change in area helps lead to the fundamental theorem
From playlist Calculus - The Fundamental Theorem of Calculus

How to Prove a Function is Injective(one-to-one) Using the Definition
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to prove a function is injective. Injective functions are also called one-to-one functions. This is a short video focusing on the proof.
From playlist Proofs

Apply the evt and find extrema on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Georg Tamme: On excision in algebraic K-theory
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Georg Tamme: On excision in algebraic K-theory Abstract: I will present a new and direct proof of a result of Suslin saying that any Tor-unital ring satisfies excision in algebraic
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Classification of n-component links with Khovanov homology of rank 2^n - Boyu Zhang
Symplectic Dynamics/Geometry Seminar Topic: Classification of n-component links with Khovanov homology of rank 2^n Speaker: Boyu Zhang Affiliation: Princeton University Date: February 24, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Limit Theorems in Pseudorandomness - Raghu Meka
Raghu Meka The University of Texas at Austin; Member, School of Mathematics October 3, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Charles Weibel: K-theory of algebraic varieties (Lecture 3)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Charles Weibel: K theory of algebraic varieties Abstract: Lecture 1 will present definitions for the Waldhausen K-theory of rings, varieties, additive and exact categories, and dg c
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Fraydoun Rezakhanlou: "Kinetic Theory for Hamilton-Jacobi PDEs"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop IV: Stochastic Analysis Related to Hamilton-Jacobi PDEs "Kinetic Theory for Hamilton-Jacobi PDEs" Fraydoun Rezakhanlou - University of California, Berkeley (UC Berkeley) Abstract: The flow of a Hamilton-Jacobi PDE yields a dynamical sys
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Mod-04 Lec-22 Continuation of Solutions
Ordinary Differential Equations and Applications by A. K. Nandakumaran,P. S. Datti & Raju K. George,Department of Mathematics,IISc Bangalore.For more details on NPTEL visit http://nptel.ac.in.
From playlist IISc Bangalore: Ordinary Differential Equations and Applications | CosmoLearning.org Mathematics

Antonio Rieser (03/29/23) Algebraic Topology for Graphs & Mesoscopic Spaces: Homotopy & Sheaf Theory
Title: Algebraic Topology for Graphs and Mesoscopic Spaces: Homotopy and Sheaf Theory Abstract: In this talk, we introduce the notion of a mesoscopic space: a metric space decorated with a privileged scale, and we survey recent developments in the algebraic topology of such spaces. Our ap
From playlist AATRN 2023

Stable Homotopy Theory by Samik Basu
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Math 176. Math of Finance. Lecture 07.
UCI Math 176: Math of Finance (Fall 2014) Lec 07. Math of Finance View the complete course: http://ocw.uci.edu/courses/math_176_math_of_finance.html Instructor: Donald Saari, Ph.D. License: Creative Commons CC-BY-SA Terms of Use: http://ocw.uci.edu/info More courses at http://ocw.uci.edu
From playlist Math 176: Math of Finance

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Tropical motivic integration - S. Payne - Workshop 2 - CEB T1 2018
Sam Payne (Yale University) / 09.03.2018 Tropical motivic integration. I will present a new tool for the calculation of motivic invariants appearing in Donaldson-Thomas theory, such as the motivic Milnor fiber and motivic nearby fiber, starting from a theory of volumes of semi-algebraic
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields