
Category Theory: The Beginner’s Introduction (Lesson 1 Video 4)
Lesson 1 is concerned with defining the category of Abstract Sets and Arbitrary Mappings. We also define our first Limit and Co-Limit: The Terminal Object, and the Initial Object. Other topics discussed include Duality and the Opposite (or Mirror) Category. These videos will be discussed
From playlist Category Theory: The Beginner’s Introduction

Introduction to Sets and Set Notation
This video defines a set, special sets, and set notation.
From playlist Sets (Discrete Math)

We give a buttload of definitions for morphisms on various categories of complexes. The derived category of an abelian category is a category whose objects are cochain complexes and whose morphisms I describe in this video.
From playlist Derived Categories

The big mathematics divide: between "exact" and "approximate" | Sociology and Pure Maths | NJW
Modern pure mathematics suffers from a major schism that largely goes unacknowledged: that many aspects of the subject are parading as "exact theories" when in fact they are really only "approximate theories". In this sense they can be viewed either as belonging more properly to applied ma
From playlist Sociology and Pure Mathematics
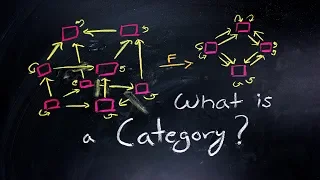
What is a Category? | Nathan Dalaklis
Categories and Functors can be pretty mindboggling mathematical objects to wrap your head around if you're not used to abstract math, but they come up as useful tools to study different structures in mathematics and beyond. So... What is a Category? Here I introduce the definition of a Cat
From playlist The New CHALKboard

Kevin Coulembier: Frobenius exact tensor categories
Abstract: Partly motivated by Grothendieck’s original vision for motives, the question arises of when a tensor category (k-linear symmetric monoidal rigid abelian category) is tannakian, i.e. is the representation category of an affine group scheme, or more generally of a groupoid in schem
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

Marco Schlichting: Introduction to Higher Grothendieck Witt groups (Lecture 2)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: Workshop "Hermitian K-theory and trace methods"
From playlist HIM Lectures: Junior Trimester Program "Topology"

Stable Homotopy Seminar, 11: Stable Model Categories and Triangulated Categories
(Note: I messed up the first recording and had to re-record the first 20 minutes of this.) I show that cofiber sequences agree with fiber sequences in Spectra, or indeed in any pointed model category where suspension is invertible. The homotopy category of such a model category is a highly
From playlist Stable Homotopy Seminar

Charles Rezk - 4/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart4.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online

Yonatan Harpaz - New perspectives in hermitian K-theory I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Algebraic K-theory, combinatorial K-theory and geometry - Inna Zakharevich
Vladimir Voevodsky Memorial Conference Topic: Algebraic K-theory, combinatorial K-theory and geometry Speaker: Inna Zakharevich Affiliation: Cornell University Date: September 14, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Commutative algebra 47: Colimits and exactness
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We discuss the question of when a colimit of exact sequences is exact. We first show that a colimit of right exact sequences i
From playlist Commutative algebra

Algebraic K-Theory Via Binary Complexes - Daniel Grayson
Daniel Grayson University of Illinois at Urbana-Champaign; Member, School of Mathematics October 22, 2012 Quillen's higher K-groups, defined in 1971, paved the way for motivic cohomology of algebraic varieties. Their definition as homotopy groups of combinatorially constructed topolo
From playlist Mathematics

Georg Tamme: On excision in algebraic K-theory
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Georg Tamme: On excision in algebraic K-theory Abstract: I will present a new and direct proof of a result of Suslin saying that any Tor-unital ring satisfies excision in algebraic
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Yonatan Harpaz - New perspectives in hermitian K-theory III
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Determine if a Relation is a Function
http://mathispower4u.wordpress.com/
From playlist Intro to Functions



