
Homomorphisms in abstract algebra
In this video we add some more definition to our toolbox before we go any further in our study into group theory and abstract algebra. The definition at hand is the homomorphism. A homomorphism is a function that maps the elements for one group to another whilst maintaining their structu
From playlist Abstract algebra

Isomorphisms in abstract algebra
In this video I take a look at an example of a homomorphism that is both onto and one-to-one, i.e both surjective and injection, which makes it a bijection. Such a homomorphism is termed an isomorphism. Through the example, I review the construction of Cayley's tables for integers mod 4
From playlist Abstract algebra
Group Isomorphisms in Abstract Algebra
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Isomorphisms in Abstract Algebra - Definition of a group isomorphism and isomorphic groups - Example of proving a function is an Isomorphism, showing the group of real numbers under addition is isomorphic to the group of posit
From playlist Abstract Algebra

Homomorphisms in abstract algebra examples
Yesterday we took a look at the definition of a homomorphism. In today's lecture I want to show you a couple of example of homomorphisms. One example gives us a group, but I take the time to prove that it is a group just to remind ourselves of the properties of a group. In this video th
From playlist Abstract algebra

Sets might contain an element that can be identified as an identity element under some binary operation. Performing the operation between the identity element and any arbitrary element in the set must result in the arbitrary element. An example is the identity element for the binary opera
From playlist Abstract algebra

Group Homomorphisms - Abstract Algebra
A group homomorphism is a function between two groups that identifies similarities between them. This essential tool in abstract algebra lets you find two groups which are identical (but may not appear to be), only similar, or completely different from one another. Homomorphisms will be
From playlist Abstract Algebra

Isomorphisms (Abstract Algebra)
An isomorphism is a homomorphism that is also a bijection. If there is an isomorphism between two groups G and H, then they are equivalent and we say they are "isomorphic." The groups may look different from each other, but their group properties will be the same. Be sure to subscribe s
From playlist Abstract Algebra

Shadows of Computation - Lecture 3 - The gap between equivalent concepts
Welcome to Shadows of Computation, an online course taught by Will Troiani and Billy Snikkers, covering the foundations of category theory and how it is used by computer scientists to abstract computing systems to reveal their intrinsic mathematical properties. In the third lecture Will sp
From playlist Shadows of Computation

Charles Rezk - 3/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart3.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online

This is video number 4 in the series defining topoi. Here's the updated text used in the video: https://gist.github.com/Nikolaj-K/469b9ca1c085ea4ac4e3d7d0008913f5 Last video: https://youtu.be/Bdn64edr4Ng
From playlist Logic

Homomorphisms (Abstract Algebra)
A homomorphism is a function between two groups. It's a way to compare two groups for structural similarities. Homomorphisms are a powerful tool for studying and cataloging groups. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦♦ W
From playlist Abstract Algebra

Charles Rezk - 4/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart4.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online
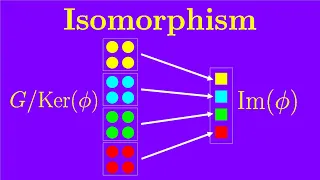
Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory
The isomorphism theorem is a very useful theorem when it comes to proving novel relationships in group theory, as well as proving something is a normal subgroup. But not many people can understand it intuitively and remember it just as a kind of algebraic coincidence. This video is about t
From playlist Essence of Group Theory

Model Theory - part 02 - Signatures, Lawvere Categories, Structures (now valued in Categories!)
I learned about this approach from Riehl in the existential context here. Her webpage is here: http://www.math.jhu.edu/~eriehl/ Also, I found the refrences by Caramello and Awodey very helpful. They build on what is done in Reyes-Makkai. Whatever Awodey writes is basically gold. Here he
From playlist Model Theory

Emily Riehl: On the ∞-topos semantics of homotopy type theory: The simplicial model of...- Lecture 2
HYBRID EVENT Recorded during the meeting "Logic and Interactions" the February 22, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual M
From playlist Topology

Mountain West Ruby 2016 - How Are Method Calls Formed? by Aaron Patterson
How Are Method Calls Formed? by Aaron Patterson today, we’ll dive in to optimizations we can make on method dispatch including various types of inline method caching. Audience members should leave with a better understanding of Ruby’s VM internals as well as ways to analyze and optimize
From playlist Mountain West Ruby 2016

Topoi 3: The definition of a topos
This is video number 3 in the series defining topoi. Here's the updated text used in the video: https://gist.github.com/Nikolaj-K/469b9ca1c085ea4ac4e3d7d0008913f5 Fourth video on Power and Negation in a topos: https://youtu.be/dvXRQI8RonY
From playlist Algebra

BathRuby 2016 - How are Method Calls Formed? by Aaron Patterson
How are Method Calls Formed? by Aaron Patterson In this presentation we're going to study how method calls are executed. We'll go from bytecode created by Ruby's Virtual Machine down to the C code where the methods actually get executed. After we've learned about how Ruby executes method
From playlist BathRuby 2016

Charles Rezk - 1/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart1.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online

Linear Algebra 8.3 Isomorphism
My notes are available at http://asherbroberts.com/ (so you can write along with me). Elementary Linear Algebra: Applications Version 12th Edition by Howard Anton, Chris Rorres, and Anton Kaul A. Roberts is supported in part by the grants NSF CAREER 1653602 and NSF DMS 2153803.
From playlist Linear Algebra