
Ever wondered what a partial sum is? The simple answer is that a partial sum is actually just the sum of part of a sequence. You can find a partial sum for both finite sequences and infinite sequences. When we talk about the sum of a finite sequence in general, we’re talking about the sum
From playlist Popular Questions

Ex: Find the Error When Using a Partial Sum to Estimate an Infinite Sum (Alternating Series)
This video explains how to find the error when using a partial sum to estimate an infinite sum of a convergent alternating series. Site: http://mathispower4u.com
From playlist Infinite Series

Ex: Number of Terms Needed in Partial Sum to Estimate an Infinite Sum with a Given Error.
This video explains how many terms are needed in a partial sum of an alternating series to estimate the infinite with a given error. Site: http://mathispower4u.com
From playlist Infinite Series

Why Excel SUM is zero. Why Excel Sum function not working. Why Excel SUM returns 0. Why Excel Sum is wrong. Why Excel Sum shows 0. Why Excel Not Showing Sum. Why Excel Sum Formula Not working. Do you have a column of numbers that won't sum in Excel? It is most likely that the numbers have
From playlist Shorts from Google Search

Indeterminate Partial Sums (1 of 2: Finding the length of the series)
More resources available at www.misterwootube.com
From playlist Modelling Financial Situations

Why Excel SUM is zero. Why Excel Sum function not working. Why Excel SUM returns 0. Why Excel Sum is wrong. Why Excel Sum shows 0. Why Excel Not Showing Sum. Why Excel Sum Formula Not working. Do you have a column of numbers that won't sum in Excel? It is most likely that the numbers have
From playlist Shorts from Google Search
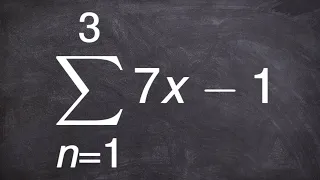
Finding the sum or an arithmetic series using summation notation
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series
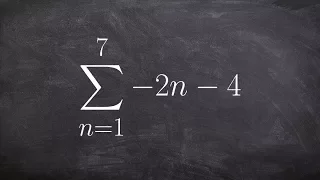
Learn to use summation notation for an arithmetic series to find the sum
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series

Kemperman's Critical Pair Theory by David Grynkiewicz
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020

MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=OHiu2F18dFA&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

Marginal triviality of the scaling limits of critical 4D Ising (Lecture 3) by Hugo Duminil-Copin
INFOSYS-ICTS RAMANUJAN LECTURES CRITICAL PHENOMENA THROUGH THE LENS OF THE ISING MODEL SPEAKER: Hugo Duminil-Copin (Institut des Hautes Études Scientifiques, France & University of Geneva, Switzerland) DATE: 09 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall Lecture 1 D
From playlist Infosys-ICTS Ramanujan Lectures

Excel Magic Trick 784: Empty Cells OR Formula Created Blank: Confusion Over Word "Blank"
Download Excel Start File: https://people.highline.edu/mgirvin/YouTubeExcelIsFun/EMT779-786.xlsm Download file: https://people.highline.edu/mgirvin/YouTubeExcelIsFun/EMT779-786.xlsm Learn about important distinction between an empty cell and an Null String (Formula Created Blank) for the
From playlist Excel Series: Magic Tricks (5th 200 videos)

SUMIFS Function: Adding with Criteria 36 Examples & SUMIF function, Excel Magic Trick 978
Download Excel Start File: https://people.highline.edu/mgirvin/YouTubeExcelIsFun/EMT978.xlsx Download Excel File: http://people.highline.edu/mgirvin/ExcelIsFun.htm Learn how to add with one or more criteria (conditions) using SUMIFS and SUMIF functions. Topics in this video can be equall
From playlist Excel Adding With Multiple Criteria Tricks

Hugo Duminil-Copin - 4/4 Triviality of the 4D Ising Model
We prove that the scaling limits of spin fluctuations in four-dimensional Ising-type models with nearest-neighbor ferromagnetic interaction at or near the critical point are Gaussian. A similar statement is proven for the λ4 fields over R4 with a lattice ultraviolet cutoff, in the limit of
From playlist Hugo Duminil-Copin - Triviality of the 4D Ising Model

Hugo Duminil-Copin: Lecture #3
Third lecture on "Marginal triviality of the scaling limits of critical 4D Ising and ϕ^4_4 models" by Professor Hugo Duminil-Copin. For more materials and slides visit: https://sites.google.com/view/oneworld-pderandom/home
From playlist Summer School on PDE & Randomness

RES.LL-005 D4M: Signal Processing on Databases, Fall 2012 View the complete course: http://ocw.mit.edu/RESLL-005F12 Instructor: Jeremy Kepner Introduction to associative arrays. D4M.mit.edu software demo example/1Intro/1AssocIntro. Creating, writing, reading, selecting, and performing mat
From playlist MIT D4M: Signal Processing on Databases, Fall 2012

What is the sum of an arithmetic series using the sum formula
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series

Extremal Combinatorics with Po-Shen Loh - 04/13 Mon
Carnegie Mellon University is protecting the community from the COVID-19 pandemic by running courses online for the Spring 2020 semester. This is the video stream for Po-Shen Loh’s PhD-level course 21-738 Extremal Combinatorics. Professor Loh will not be able to respond to questions or com
From playlist CMU PhD-Level Course 21-738 Extremal Combinatorics

