
Gaussian Integral 7 Wallis Way
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I calculate the Gaussian integral by using a technique that is very similar to the
From playlist Gaussian Integral

Gaussian Integral 8 Original Way
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I present the classical way using polar coordinates, the one that Laplace original
From playlist Gaussian Integral

Gaussian Integral 6 Gamma Function
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I calculate the Gaussian integral by using properties of the gamma function, which
From playlist Gaussian Integral

Riemann Sum Defined w/ 2 Limit of Sums Examples Calculus 1
I show how the Definition of Area of a Plane is a special case of the Riemann Sum. When finding the area of a plane bound by a function and an axis on a closed interval, the width of the partitions (probably rectangles) does not have to be equal. I work through two examples that are rela
From playlist Calculus

Quantum Integral. Gauss would be proud! I calculate the integral of x^2n e^-x^2 from -infinity to infinity, using Feynman's technique, as well as the Gaussian integral and differentiation. This integral appears over and over again in quantum mechanics and is useful for calculus and physics
From playlist Integrals

Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I calculate the Gaussian integral by using a Fubini-type argument, namely by calcu
From playlist Gaussian Integral

Gaussian Integral 9 Stirling Way
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I use Stirling's formula to 'prove' the Gaussian integral, namely I show that in t
From playlist Gaussian Integral

Gaussian Integral 11 Complex Analysis
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I use complex analysis to calculate the Gaussian integral. More precisely, I integ
From playlist Gaussian Integral

8ECM Plenary Lecture: Umberto Zannier
From playlist 8ECM Plenary Lectures

Potential automorphy of Ĝ-local systems – Jack Thorne – ICM2018
Number Theory Invited Lecture 3.12 Potential automorphy of Ĝ-local systems Jack Thorne Abstract: Vincent Lafforgue has recently made a spectacular breakthrough in the setting of the global Langlands correspondence for global fields of positive characteristic, by constructing the ‘automor
From playlist Number Theory

Fermat's Last Theorem - The Theorem and Its Proof: An Exploration of Issues and Ideas [1993]
supplement to the video: http://www.msri.org/realvideo/ln/msri/1993/outreach/fermat/1/banner/01.html Date: July 28, 1993 (08:00 AM PDT - 09:00 AM PDT) Fermat's Last Theorem July 28, 1993, Robert Osserman, Lenore Blum, Karl Rubin, Ken Ribet, John Conway, and Lee Dembart. Musical interlude
From playlist Number Theory
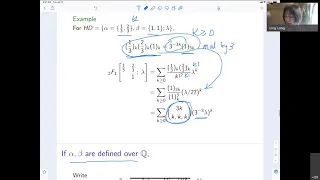
Ling Long - Hypergeometric Functions, Character Sums and Applications - Lecture 4
Title: Hypergeometric Functions, Character Sums and Applications Speaker: Prof. Ling Long, Louisiana State University Abstract: Hypergeometric functions form a class of special functions satisfying a lot of symmetries. They are closely related to the arithmetic of one-parameter families of
From playlist Hypergeometric Functions, Character Sums and Applications

Simultaneous non-vanishing of L-values by Soumya Das
12 December 2016 to 22 December 2016 VENUE Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution. An
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Undecidability Tangent (History of Undecidability Part 1) - Computerphile
What was the first undecidable problem? Professor Brailsford takes us on a computerphile tangent & gives us his angle on a pre-computer example of undecidability. Note from Professor Brailsford: a couple of corrections for this film: 1/ "... early 18th Century" for Gauss should be " ... e
From playlist The History of Undecidability

Physics - E&M: Maxwell's Equations (9 of 30) Differential Form of Gauss' Law: 1
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain Gauss' Law in differential form.
From playlist PHYSICS 46 MAXWELL'S EQUATIONS

SummerSchool "Arithmetic geometry" Tschinkel - Introduction | 2006
lecture notes: https://drive.google.com/file/d/1VLucSK53-iLrVUbPAanNZ6Lb7nAAgaQ1/view?usp=sharing Clay Mathematics Institute Summer School 2006 on "Arithmetic geometry" survey lectures given at the 2006 Clay Summer School on Arithmetic Geometry at the Mathematics Institute of the Univer
From playlist Clay Mathematics Institute Summer School 2006 on "Arithmetic geometry"

Arithmetic Statistics - Lecture 1/4 by Álvaro Lozano Robledo [CTNT 2018]
Full playlist: https://www.youtube.com/playlist?list=PLJUSzeW191Qwpyp4wKvuoyQrZmfnmEWCT Notes: https://ctnt-summer.math.uconn.edu/wp-content/uploads/sites/1632/2018/06/CTNT-2018-Arithmetic-Statistics-Lecture-1.pdf Mini-course B: “Arithmetic Statistics” by Álvaro Lozano-Robledo (UConn).
From playlist Number Theory

CTNT 2018 - "Arithmetic Statistics" (Lecture 1) by Álvaro Lozano-Robledo
This is lecture 1 of a mini-course on "Arithmetic Statistics", taught by Álvaro Lozano-Robledo, during CTNT 2018, the Connecticut Summer School in Number Theory. For more information about CTNT and other resources and notes, see https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2018 - "Arithmetic Statistics" by Álvaro Lozano-Robledo

Gaussian Integral 10 Fourier Way
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out! In this video, I show how the Gaussian integral appears in the Fourier transform: Namely if you t
From playlist Gaussian Integral

Asymptotics of number fields - Manjul Bhargava [2011]
Asymptotics of number fields Introductory Workshop: Arithmetic Statistics January 31, 2011 - February 04, 2011 January 31, 2011 (11:40 AM PST - 12:40 PM PST) Speaker(s): Manjul Bhargava (Princeton University) Location: MSRI: Simons Auditorium http://www.msri.org/workshops/566
From playlist Number Theory