
Verdier And Grothendieck Duality (Lecture 4) by Suresh Nayak
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Schemes 48: The canonical sheaf
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we define the canonical sheaf, giev a survey of some applications (Riemann-Roch theorem, Serre duality, canonical embeddings, Kodaira dimensio
From playlist Algebraic geometry II: Schemes
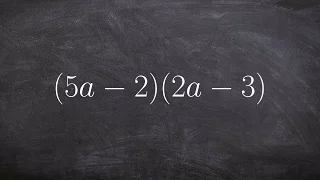
Using foil to Multiply Two Binomials - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

From Cohomology to Derived Functors by Suresh Nayak
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Sam Raskin - 2/2 What does geometric Langlands mean to a number theorist?
Sam Raskin (Univ. Texas)
From playlist 2022 Summer School on the Langlands program

Felix Klein Lecture 2022 part6
From playlist Felix Klein Lectures 2022

How to Multiply Two Monomials by a Trinomial and Binomial
👉 Learn how to multiply polynomials. We apply the distributive property to polynomials by multiplying a monomial to every term in a polynomial. When multiplying monomials it is important that we multiply the coefficients and apply the rules of exponents to add the powers of each variable.
From playlist How to Multiply Polynomials
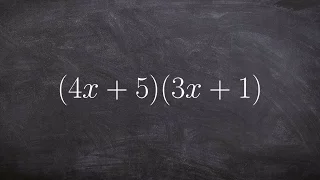
Multiplying Two Binomials Together Using the Box Method - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials
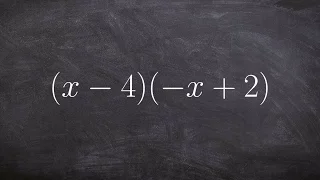
Multiplying Two Binomials - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials
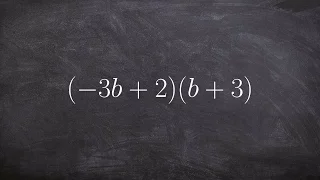
Multiplying Two Binomials - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

This video provided several examples of how to multiply two binomials. Complete Video Library: http://www.mathispower4u.com Search by Topic: htth://www.mathispower4u.wordpress.com
From playlist Multiplying Polynomials

Rahul Pandharipande - Enumerative Geometry of Curves, Maps, and Sheaves 1/5
The main topics will be the intersection theory of tautological classes on moduli space of curves, the enumeration of stable maps via Gromov-Witten theory, and the enumeration of sheaves via Donaldson-Thomas theory. I will cover a mix of classical and modern results. My goal will be, by th
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory
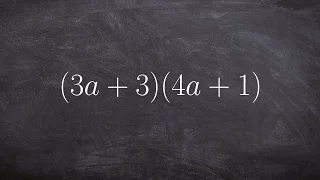
Multiply Two Binomials Using FOIL - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Mihnea Popa: Hodge filtration and birational geometry
CONFERENCE Recorded during the meeting "D-Modules: Applications to Algebraic Geometry, Arithmetic and Mirror Symmetry" the April 14, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by
From playlist Algebraic and Complex Geometry
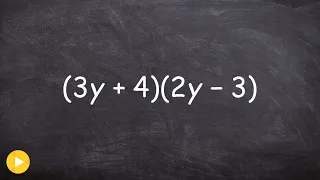
Multiplying Two Binomials Using Box Method - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Easiest Way To Multiply Two Binomials Using Foil - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Grothendieck-Serre Duality by Suresh Nayak
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Christophe Soulé - 2/4 On the Arakelov theory of arithmetic
Let X be a semi-stable arithmetic surface of genus at least two and $\omega$ the relative dualizing sheaf of X, equipped with the Arakelov metric. Parshin and Moret-Bailly have conjectured an upper bound for the arithmetic self-intersection of $\omega$. They proved that a weak form of th
From playlist Christophe Soulé - On the Arakelov theory of arithmetic surfaces

Christophe Soulé - 1/4 On the Arakelov theory of arithmetic
Let X be a semi-stable arithmetic surface of genus at least two and $\omega$ the relative dualizing sheaf of X, equipped with the Arakelov metric. Parshin and Moret-Bailly have conjectured an upper bound for the arithmetic self-intersection of $\omega$. They proved that a weak form of th
From playlist Christophe Soulé - On the Arakelov theory of arithmetic surfaces
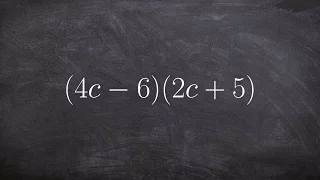
Multiplying Two Binomials - Math Tutorial - Polynomial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials