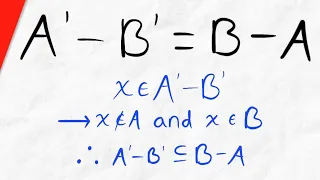
Proof: A'-B' = B-A (Double Inclusion) | Set Theory
We prove A'-B'=B-A. That is, the complement of A minus the complement of B equals B minus A. We prove this using double inclusion, meaning we prove both sets are subsets of each other, which by definition establishes set equality. This will require basic applications of set theory definiti
From playlist Set Theory

Double Complement of a Set | Set Theory
What is the complement of the complement of a set? In today's set theory lesson we'll discuss double complements with respect to "absolute complements - being complements taken with respect to a universal set as opposed to relative complements. When we consider a universal set, every oth
From playlist Set Theory

How to use Double Inclusion to Prove Two Sets are Equal: (A u B) n A^c = B\A
How to use Double Inclusion to Prove Two Sets are Equal: (A u B) n A^c = B\A
From playlist Set Theory

What is the complement of a set? Sets in mathematics are very cool, and one of my favorite thins in set theory is the complement and the universal set. In this video we will define complement in set theory, and in order to do so you will also need to know the meaning of universal set. I go
From playlist Set Theory
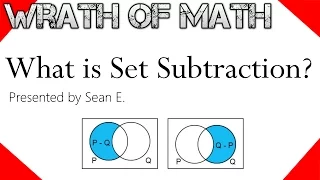
What is set subtraction? In this video we go over that, the set minus set operation, and an example of subtraction in set theory. This is a handy concept to grasp to understand the complement of a set and universal sets, which I also have videos on. Links below. I hope you find this vide
From playlist Set Theory

Set Theory 1.1 : Axioms of Set Theory
In this video, I introduce the axioms of set theory and Russel's Paradox. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/5ITQHUW
From playlist Set Theory

Introduction to sets || Set theory Overview - Part 2
A set is the mathematical model for a collection of different things; a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other #sets. The #set with no element is the empty
From playlist Set Theory

Eric Goubault, École Polytechnique
April 5, Eric Goubault, École Polytechnique Reachability and invariance for the verification of control systems, some directions
From playlist Spring 2022 Online Kolchin seminar in Differential Algebra

Introduction to sets || Set theory Overview - Part 1
A set is the mathematical model for a collection of different things; a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other #sets. The #set with no element is the empty
From playlist Set Theory

Double covers of tori and the local Langlands correspondence - Tasho Kaletha
Workshop on Representation Theory and Geometry Topic: Double covers of tori and the local Langlands correspondence Speaker: Tasho Kaletha Affiliation: University of Michigan Date: April 02, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

What are Overlapping Sets? | Set Theory
What are overlapping sets? This is a relation between sets that I have not seen any YouTube videos on, so I figured I'd add this video explaining the term to the massive YouTube catalogue! In this video we define overlapping sets and give some examples. Two sets, A and B, are overlapping
From playlist Set Theory

Galois Representations 1 by Shaunak Deo
PROGRAM : ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (ONLINE) ORGANIZERS : Ashay Burungale (California Institute of Technology, USA), Haruzo Hida (University of California, Los Angeles, USA), Somnath Jha (IIT - Kanpur, India) and Ye Tian (Chinese Academy of Sciences, China) DA
From playlist Elliptic Curves and the Special Values of L-functions (ONLINE)
John Pardon, Smoothing finite group actions on three-manifolds
2018 Clay Research Conference, CMI at 20
From playlist CMI at 20

Moduli of p-divisible groups (Lecture 3) by Ehud De Shalit
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Ralf Schindler Universität Münster, Germany
From playlist Talks of Mathematics Münster's reseachers

From Coxeter Higher-Spin Theories to Strings and Tensor Models by Mikhail Vasiliev
ORGANIZERS : Pallab Basu, Avinash Dhar, Rajesh Gopakumar, R. Loganayagam, Gautam Mandal, Shiraz Minwalla, Suvrat Raju, Sandip Trivedi and Spenta Wadia DATE : 21 May 2018 to 02 June 2018 VENUE : Ramanujan Lecture Hall, ICTS Bangalore In the past twenty years, the discovery of the AdS/C
From playlist AdS/CFT at 20 and Beyond

Visual Group Theory, Lecture 6.7: Ruler and compass constructions
Visual Group Theory, Lecture 6.7: Ruler and compass constructions Inspired by philosophers such as Plato and Aristotle, one of the chief purposes of ancient Greek mathematics was to find exact constructions for various lengths, using only the basic tools of a ruler and compass. However, t
From playlist Visual Group Theory

Mod-05 Lec-36 Subgame Perfect Nash Equilibrium
Game Theory and Economics by Dr. Debarshi Das, Department of Humanities and Social Sciences, IIT Guwahati. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist IIT Guwahati: Game Theory and Economics | CosmoLearning.org Economics

Rings 12 Duality and injective modules
This lecture is part of an online course on rings and modules. We descibe some notions of duality for modules generalizing the dual of a vector space. We first discuss duality for free and projective modules, which is very siilar to the vector space case. Then we discuss duality for finit
From playlist Rings and modules

Proving Two Sets are Equal using Double Inclusion: A u (A n B) = A
Proving Two Sets are Equal using Double Inclusion: A u (A n B) = A
From playlist Set Theory