
How to Construct a Dodecahedron
How the greeks constructed the Dodecahedron. Euclids Elements Book 13, Proposition 17. In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. A regular dode
From playlist Platonic Solids

Canonical structures inside the Platonic solids III | Universal Hyperbolic Geometry 51
The dodecahedron is surely one of the truly great mathematical objects---revered by the ancient Greeks, Kepler, and many mathematicians since. Its symmetries are particularly rich, and in this video we look at how to see the five-fold and six-fold symmetries of this object via internal str
From playlist Universal Hyperbolic Geometry

Post-it Note Dodecahedron: Your Photos
From playlist My Maths Videos

Area of dodecagon from a square!
This is a short, animated visual proof demonstrating that the area of a regular dodecagon inscribed in the unit circle has an area of exactly 3. #math #manim #visualproof #mathvideo #geometry #mathshorts #geometry #mtbos #animation #theorem #pww #proofwithoutwords #proof #it
From playlist MathShorts
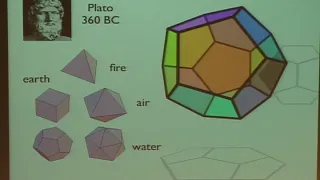
Mathematics as Metaphor - Curtis McMullen (Harvard University)
Public lecture
From playlist Mathematics Research Center

In this veideo we continue our look in to the dihedral groups, specifically, the dihedral group with six elements. We note that two of the permutation in the group are special in that they commute with all the other elements in the group. In the next video I'll show you that these two el
From playlist Abstract algebra

Dodecahedron in Geogebra Step by step tutorial on this link: https://youtu.be/FPDOfPhheFk In case you wanna to pay me a drink: https://www.paypal.me/admirsuljicic/
From playlist Geogebra [Tutoriali]
GraphData: New Developments and Research Applications
GraphData is an extensive curated database of simple graphs and their properties available in Mathematica as a built-in data paclet and in Wolfram|Alpha via natural language queries. GraphData was first introduced in Mathematica Version 6, and the number of graphs, property count, and frac
From playlist Wolfram Technology Conference 2013

Combinatorics and Geometry to Arithmetic of Circle Packings - Nakamura
Speaker: Kei Nakamura (Rutgers) Title: Combinatorics and Geometry to Arithmetic of Circle Packings Abstract: The Koebe-Andreev-Thurston/Schramm theorem assigns a conformally rigid fi-nite circle packing to a convex polyhedron, and then successive inversions yield a conformally rigid infin
From playlist Mathematics

A fold-up, slice-and-dice dodecahedron and its complement. With a 3D printer, you can make your own using the files here: http://georgehart.com/rp/T-O-M/t-o-m.html
From playlist Odds and Ends

Dodecaplex: the puzzle from the fourth dimension!
Check out Dodecaplex on Maths Gear! https://mathsgear.co.uk/products/dodecaplex-puzzle Dodecaplex is based on the mathematics of Saul Schleimer and Henry Segerman. Henry Segerman http://www.segerman.org/ Saul Schleimer http://homepages.warwick.ac.uk/~masgar/ You can read more about the
From playlist Guest appearances

The unexpected logic behind rolling multiple dice and picking the highest.
Check out Jane Street's icosahedron puzzle: https://www.janestreet.com/IMO2022/ 2022 International Mathematical Olympiad! https://www.imo2022.org/ If you want those d60 and d120 we sell them on Maths Gear or you can go direct to The Dice Lab. https://mathsgear.co.uk/collections/dice http
From playlist Prob and Stats

Regular dodecagon surprises. How to prove? Source: Antonio Gutierrez. https://geogebra.org/m/wxywrnwh #GeoGebra #MTBoS #ITeachMath #geometry #math #maths #proof #ProofWithoutWords #EdTech #MathChat #GeomChat
From playlist Geometry: Challenge Problems

This shows a 3d print of a puzzle I produced using shapeways.com. This is joint work with Saul Schleimer. This is available at http://shpws.me/lmxi. A larger version of the puzzle is available at http://shpws.me/lmxi.
From playlist 3D printing

Available from Shapeways: https://www.shapeways.com/shops/henryseg?section=Holonomy+mazes Thanks to Sabetta Matsumoto and Chaim Goodman-Strauss for building the sculpture, to Saul Schleimer for naming the "rook", and to all of them for helpful conversations.
From playlist 3D printing

How do ceramic crystal structures differ from metal crystal structures?
Metal crystal structures are much simpler than ceramic structures. This is due to two reasons. First, ceramics have positive and negative charged ions. Cations and ions must maintain charge neutrality. Second, the size of cations and anions are very different! Structures with multiple diff
From playlist Materials Sciences 101 - Introduction to Materials Science & Engineering 2020

To Build Viruses: A Markov Chain Monte Carlo Algorithm for Stimulating Viral Assembly Kinetics
For the latest information, please visit: http://www.wolfram.com Speaker: Nicholas Brunk Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and more.
From playlist Wolfram Technology Conference 2015

Ian Agol, Lecture 3: Applications of Kleinian Groups to 3-Manifold Topology
24th Workshop in Geometric Topology, Calvin College, June 30, 2007
From playlist Ian Agol: 24th Workshop in Geometric Topology

Bridges 2014 talk: The quaternion group as a symmetry group
This is a talk I gave at the Bridges conference on mathematics and the arts (http://bridgesmathart.org/), on 18th August 2014, about my paper with Vi Hart with the same title. The slides are available at https://www.math.okstate.edu/~segerman/talks/quaternion_group_as_a_symmetry_group.pdf
From playlist 3D printing

Demolition with dodecahedrons of various masses, trajectories, and velocities.
From playlist Physics