
This video explains what is taught in discrete mathematics.
From playlist Mathematical Statements (Discrete Math)

Discrete Structures, Oct 20: Counting
Combinations, Permutations, Pigeonhole Principle
From playlist Discrete Structures

Discrete Math - 9.3.1 Matrix Representations of Relations and Properties
How to represent a relation using a matrix and easy tips for determining if the relation is reflexive, irreflexive, symmetric, antisymetric, asymmetric and transitive. Matrix operations are also reviewed (meet, join and Boolean product). Textbook: Rosen, Discrete Mathematics and Its Appl
From playlist Discrete Math I (Entire Course)

Maths for Programmers: Introduction (What Is Discrete Mathematics?)
Transcript: In this video, I will be explaining what Discrete Mathematics is, and why it's important for the field of Computer Science and Programming. Discrete Mathematics is a branch of mathematics that deals with discrete or finite sets of elements rather than continuous or infinite s
From playlist Maths for Programmers

Intro to Discrete Math - Welcome to the Course!
Welcome to Discrete Math. This is the start of a playlist which covers a typical one semester class on discrete math. I chat a little about why I love discrete math, what you should expect, and how an online discrete math course is structured. FULL PLAYLIST: https://www.youtube.com/watch
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)

The formal definition of a sequence.
We have an intuitive picture of sequences (infinite ordered lists). But there is a formal definition of sequences based out of the idea of a specific function between sets, specifically from the positive integers to the real numbers. ►Full DISCRETE MATH Course Playlist: https://www.youtu
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)
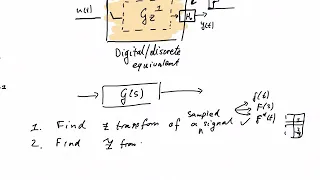
Connecting discrete and continuous systems
To have an effect in the real world, discrete systems have to sample sample continuous signals to operate on them and reconstruct their outputs to continuous signals. This video explains this and the problems associated with the z transform
From playlist Discrete

Lecture 11: Discrete Curves (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Adventures in Gapless Topological Phases - Ryan Thorngren
High Energy Theory Seminar Topic: Adventures in Gapless Topological Phases Speaker: Ryan Thorngren Affiliation: Harvard University Date: November 09, 2020 For more video please visit http://video.ias.edu Thorngren-2020-11-09
From playlist IAS High Energy Theory Seminar

Yang Shi: Normalizer theory of Coxeter groups and discrete integrable systems
Abstract: Formulation of the Painleve equations and their generalisations as birational representations of affine Weyl groups provides us with an elegant and efficient way to study these highly transcendental, nonlinear equations. In particular, it is well-known that discrete evolutions of
From playlist Integrable Systems 9th Workshop

Chiral Lattice Theories from Staggered Fermions by Simon Catterall
PROGRAM Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography (ONLINE) ORGANIZERS: David Berenstein (UCSB), Simon Catterall (Syracuse University), Masanori Hanada (University of Surrey), Anosh Joseph (IISER, Mohali), Jun Nishimura (KEK Japan), David Sc
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography (Online)

Lattice Supersymmetric Field Theories (Lecture 1) by David Schaich
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Vortices and Generalised Symmetry by Mathew Bullimore
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Lec 9 | MIT RES.6-008 Digital Signal Processing, 1975
Lecture 9: The discrete Fourier transform Instructor: Alan V. Oppenheim View the complete course: http://ocw.mit.edu/RES6-008S11 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT RES.6-008 Digital Signal Processing, 1975

Group Foliation of Finite Difference Equations Using Equivariant Moving Frames
From playlist Spring 2018

Symmetries in QFT and Their Relationship With Category Theory (Lecture 1) by Lakshya Bhardwaj
INFOSYS-ICTS STRING THEORY LECTURES SYMMETRIES IN QFT AND THEIR RELATIONSHIP WITH CATEGORY THEORY SPEAKER Lakshya Bhardwaj (Mathematical Institute, University of Oxford) DATE & TIME 10 October 2022 to 12 October 2022 VENUE Madhava Lecture Hall (Hybrid) Lecture 1: 10 October 2022 at 3:30 p
From playlist Infosys-ICTS String Theory Lectures

Progress and Prospects of Lattice Supersymmetry by David Schaich
PROGRAM Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography (ONLINE) ORGANIZERS: David Berenstein (UCSB), Simon Catterall (Syracuse University), Masanori Hanada (University of Surrey), Anosh Joseph (IISER, Mohali), Jun Nishimura (KEK Japan), David Sc
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography (Online)

[Discrete Mathematics] Finite State Machines
We do a quick introduction to finite state machines, creating our own, understanding what they do, and abstracting the purpose of these machines. Visit our website: http://bit.ly/1zBPlvm Subscribe on YouTube: http://bit.ly/1vWiRxW *--Playlists--* Discrete Mathematics 1: https://www.youtu
From playlist Discrete Math 1

