
What is the discriminant and what does it mean
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About
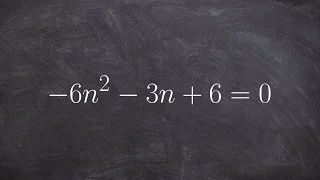
How to use the discriminat to describe your solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation
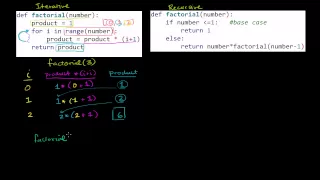
Comparing Iterative and Recursive Factorial Functions
Comparing iterative and recursive factorial functions
From playlist Computer Science
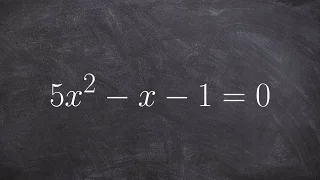
Determine and describe the discriminant
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

How to find the discriminant of a quadratic and label the solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

Overview of solutions of a quadratic function and the discriminant
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About
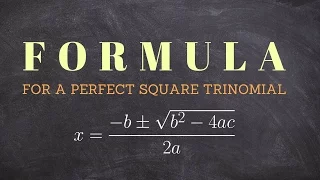
What is the formula for a perfect square trinomial and how does the discriminant fit in
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About
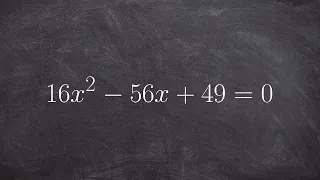
How to find the discriminant and label the solutions of a quadratic
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

Dmitriy Bilyk: On the interplay between uniform distribution,discrepancy, and energy
VIRTUAL LECTURE Recording during the meeting "Discrepancy Theory and Applications". Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywo
From playlist Analysis and its Applications

Florian Pausinger: From the discrepancy of stratified samples togreedy energy minimization
VIRTUAL LECTURE Recording during the meeting "Discrepancy Theory and Applications". Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywo
From playlist Jean-Morlet Chair - Tichy/Rivat

Terence Tao - The Erdős discrepancy problem [2017]
slides for this talk: https://drive.google.com/file/d/1rlGcmAWUFysSbNi6vMbrbhPyQewqDash/view?usp=sharing Terence Tao (UCLA) 2017-06-15 The Erdős discrepancy problem Many basic PDE of physical interest, such as the three-dimensional Navier-Stokes equations, are "supercritical" in that t
From playlist Mathematics
Dmitryi Bilyk: Uniform distribution, lacunary Fourier series, and Riesz products
Uniform distribution theory, which originated from a famous paper of H. Weyl, from the very start has been closely connected to Fourier analysis. One of the most interesting examples of such relations is an intricate similarity between the behavior of discrepancy (a quantitative measure of
From playlist HIM Lectures: Trimester Program "Harmonic Analysis and Partial Differential Equations"

NIPS 2011 Domain Adaptation Workshop: Discrepancy and Adaptation
Domain Adaptation Workshop: Theory and Application at NIPS 2011 Invited Talk: Discrepancy and Adaptation by Mehryar Mohri Mehryar Mohri is a Professor at the Courant Institute and a Research Consultant at Google. His current research interests include machine learning, computational
From playlist NIPS 2011 Domain Adaptation Workshop

Robert Tichy: Metric Discrepancy Theory
CIRM HYBRID EVENT Recorded during the meeting " Diophantine Problems, Determinism and Randomness" the February 04, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathem
From playlist Analysis and its Applications

What does the discriminant tell us about the solutions of a quadratic equation
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About

Florian Pausinger: Part 3: Greedy energy minimization and thevan der Corput sequence
VIRTUAL LECTURE Recording during the meeting "Discrepancy Theory and Applications". Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywo
From playlist Jean-Morlet Chair - Tichy/Rivat

Discrepancy of generalized polynomials by Anirban Mukhopadhyay
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020

Robert Tichy: Quasi-Monte Carlo methods and applications: introduction
VIRTUAL LECTURE Recording during the meeting "Quasi-Monte Carlo Methods and Applications " the October 28, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician
From playlist Virtual Conference

(New Version Available) Inverse Functions
New Version: https://youtu.be/q6y0ToEhT1E Define an inverse function. Determine if a function as an inverse function. Determine inverse functions. http://mathispower4u.wordpress.com/
From playlist Exponential and Logarithmic Expressions and Equations

Gunther Leobacher: Quasi Monte Carlo Methods and their Applications
In the first part, we briefly recall the theory of stochastic differential equations (SDEs) and present Maruyama's classical theorem on strong convergence of the Euler-Maruyama method, for which both drift and diffusion coefficient of the SDE need to be Lipschitz continuous. VIRTUAL LECTU
From playlist Virtual Conference