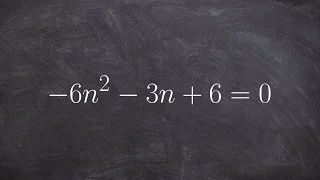
How to use the discriminat to describe your solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

What is the discriminant and what does it mean
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About

This lecture is part of an online graduate course on Galois theory. We define the discriminant of a finite field extension, ans show that it is essentially the same as the discriminant of a minimal polynomial of a generator. We then give some applications to algebraic number fields. Corr
From playlist Galois theory

How to find the discriminant of a quadratic and label the solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation
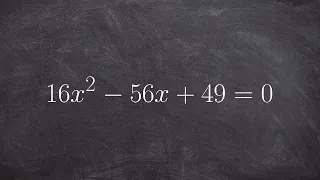
How to find the discriminant and label the solutions of a quadratic
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation
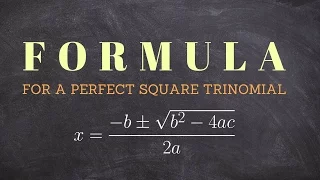
What is the formula for a perfect square trinomial and how does the discriminant fit in
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About
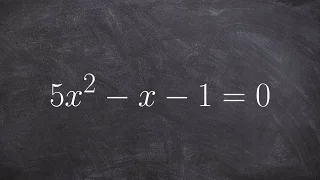
Determine and describe the discriminant
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

Rima Chatterjee: Structure Theorems of Legendrian Knots in Contact Manifolds
Rima Chatterjee, University of Cologne Title: Structure Theorems of Legendrian Knots in Contact Manifolds Structure theorems of a Legendrian knot have been an interesting study in contact geometry. One can ask when topological operations on a knot gives us important information about the g
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

John McCarthy: Norm-preserving extensions of bounded holomorphic functions
Recording during the meeting "Interpolation in Spaces of Analytic Functions" the November 18, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audio
From playlist Analysis and its Applications

Lectures on compactness in the ̄∂–Neumann problem (Lecture 5) by Emil Straube
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019
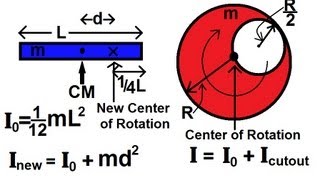
Physics - Mechanics: Application of Moment of Inertia (3 of 3) Parallel Axis Theorem
Visit http://ilectureonline.com for more math and science lectures! In this second of the three part series I will show 2 examples of moment of inertia using the Parallel Axis Theorem.
From playlist MOST POPULAR VIDEOS

Mathematical Research Lecture -- Kyle Broder -- Curvature and Moduli
A recent talk I gave concerning the link between the curvature of the total space of a family of compact complex manifolds and the moduli-theoretic behaviour of the fibres. Part of this research appears in my Ph.D. thesis, and will appear in an upcoming preprint. 💪🙏 Support the channel b
From playlist Research Lectures

Ahlfors Bers 2014 "The complex geometry of Teichmüller space and symmetric domains"
Stergios Antonakoudis (Cambridge University): From a complex analytic perspective, Teichmüller spaces can be realized as contractible bounded domains in complex vector spaces by the Bers embeddings. Bounded Symmetric domains constitute another class of bounded domains that has been extensi
From playlist The Ahlfors-Bers Colloquium 2014 at Yale

[BOURBAKI 2018] 31/03/2018 - 1/3 - Gabriel RIVIÈRE
Gabriel RIVIÈRE — Dynamique de l'équation de Schrödinger sur le disque (d'après Anantharaman, Léautaud et Macià) Dans une série de travaux récents, Anantharaman, Fermanian–Kammerer, Léautaud et Macià ont développé des outils d’analyse semi–classique afin d’étudier la dynamique en temps lo
From playlist BOURBAKI - 2018

Overview of solutions of a quadratic function and the discriminant
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About

Symplectic embeddings, integrable systems and billiards - Vinicius Ramos
Symplectic Dynamics/Geometry Seminar Topic: Symplectic embeddings, integrable systems and billiards Speaker: Vinicius Ramos Affiliation: Member, School of Mathematics Date: January 27, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Lagrangian Floer theory (Lecture – 02) by Sushmita Venugopalan
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

From playlist Complex Analysis Made Simple

What does the discriminant tell us about the solutions of a quadratic equation
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About