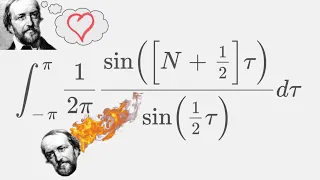Fourier series | Articles containing proofs | Mathematical analysis | Approximation theory
Dirichlet kernel
In mathematical analysis, the Dirichlet kernel, named after the German mathematician Peter Gustav Lejeune Dirichlet, is the collection of functions defined as where n is any nonnegative integer. The kernel functions are periodic with period . The importance of the Dirichlet kernel comes from its relation to Fourier series. The convolution of Dn(x) with any function f of period 2π is the nth-degree Fourier series approximation to f, i.e., we have whereis the kth Fourier coefficient of f. This implies that in order to study convergence of Fourier series it is enough to study properties of the Dirichlet kernel. (Wikipedia).