
(0.3.101) Exercise 0.3.101: Classifying Differential Equations
This video explains how to classify differential equations based upon their properties https://mathispower4u.com
From playlist Differential Equations: Complete Set of Course Videos
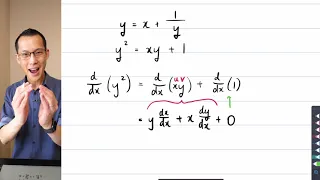
Differentiating a Continued Fraction
More resources available at www.misterwootube.com
From playlist Differential Calculus (related content)

A01 Introduction to linear systems
An introduction to linear sets of ordinary differential equations.
From playlist A Second Course in Differential Equations

Determine if the Functions are Linearly Independent or Linearly Dependent
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to determine if three functions are linearly independent or linearly dependent using the definition.
From playlist Differential Equations

C34 Expanding this method to higher order linear differential equations
I this video I expand the method of the variation of parameters to higher-order (higher than two), linear ODE's.
From playlist Differential Equations

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

C17 Non homogeneous higher order linear ODEs with constant coefficients
Explanation of the methods involved in solving a non-homogeneous, linear, ODE, with constant coefficients.
From playlist Differential Equations

Introduction to differential equations | Lecture 1 | Differential Equations for Engineers
Classification of differential equations into ode/pde, order, linear/nonlinear. Some examples are explained. Join me on Coursera: https://www.coursera.org/learn/differential-equations-engineers Lecture notes at http://www.math.ust.hk/~machas/differential-equations-for-engineers.pdf Subs
From playlist Differential Equations for Engineers

Winter School JTP: Introduction to A-infinity structures, Bernhard Keller, Lecture 3
In this minicourse, we will present basic results on A-infinity algebras, their modules and their derived categories. We will start with two motivating problems from representation theory. Then we will briefly present the topological origin of A-infinity structures. We will then define and
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Michael Mandell: The strong Kunneth theorem for topological periodic cyclic homology
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Hesselholt has recently been advertising "topological periodic cyclic homology" (TP) as potentially filling some of the same roles for finite primes as periodic cyclic homology plays
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Microlocal sheaves III: Regular singularities and Riemann-Hilbert - Michael McBreen
SL2 Seminar Topic: Microlocal sheaves III: Regular singularities and Riemann-Hilbert Speaker: Michael McBreen Affiliation: Chinese University of Hong Kong Date: March 23, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

What are differential equations?
► My Differential Equations course: https://www.kristakingmath.com/differential-equations-course Differential equations are usually classified into two general categories: partial differential equations, which are also called partial derivatives, and ordinary differential equations. Part
From playlist Popular Questions

2-Verma modules - Gregoire Naisse; Pedro Vaz
Virtual Workshop on Recent Developments in Geometric Representation Theory Topic: 2-Verma modules Speakers: Gregoire Naisse; Pedro Vaz Affiliation: University College London; University College London Date: November 18, 2020 For more video please visit http://video.ias.edu
From playlist Virtual Workshop on Recent Developments in Geometric Representation Theory

This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We define the cotangent sheaf of a scheme, and calculate it for the projective line and then for general projective space.
From playlist Algebraic geometry II: Schemes

Lecture 4: The Connes operator on HH
Correction: The formula we give for the Connes operator B is slightly wrong, there needs to be a '+' instead of a '-' in between the two summands. In this video, we discuss the Connes operator on Hochschild homology. Feel free to post comments and questions at our public forum at https:
From playlist Topological Cyclic Homology

Ben Elias: Categorifying Hecke algebras at prime roots of unity
Thirty years ago, Soergel changed the paradigm with his algebraic construction of the Hecke category. This is a categorification of the Hecke algebra at a generic parameter, where the parameter is categorified by a grading shift. One key open problem in categorification is to categorify He
From playlist Workshop: Monoidal and 2-categories in representation theory and categorification

On the notion of λ-connection - Carlos Simpson
Geometry and Arithmetic: 61st Birthday of Pierre Deligne Carlos Simpson University of Nice October 18, 2005 Pierre Deligne, Professor Emeritus, School of Mathematics. On the occasion of the sixty-first birthday of Pierre Deligne, the School of Mathematics will be hosting a four-day confe
From playlist Pierre Deligne 61st Birthday

Zhaoting Wei: Determinant line bundles and cohesive modules
Talk by Zhaoting Wei in Global Noncommutative Geometry Seminar (Americas) https://www.math.wustl.edu/~xtang/NCG-Seminar on December 16, 2020
From playlist Global Noncommutative Geometry Seminar (Americas)

A16 The method of variation of parameters
Starting the derivation for the equation that is used to find the particular solution of a set of differential equations by means of the variation of parameters.
From playlist A Second Course in Differential Equations

Michel Dubois-Violette: The Weil algebra of a Hopf algebra
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra