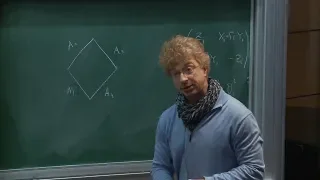What is an Included Side of a Triangle - Congruent Triangles
👉 Learn about the included angles of a triangle. An included angle of a triangle is the angle between two sides of a triangle. An included side of a triangle is the side between two angles. To show that two triangles are congruent by the side angle side (SAS) congruency theorem, we must s
From playlist Congruent Triangles

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - Philippe Nabonnand - 17/11/17
En partenariat avec le séminaire d’histoire des mathématiques de l’IHP Élie Cartan suit le cours de géométrie de Gaston Darboux Philippe Nabonnand, Archives Henri Poincaré, Université de Lorraine) À l’occasion du centenaire de la mort de Gaston Darboux, l’Institut Henri Poincaré souhaite
From playlist Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - 17/11/2017

Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - Barnabé Croizat - 17/11/17
En partenariat avec le séminaire d’histoire des mathématiques de l’IHP Ovales, cyclides et surfaces orthogonales : les premières amours géométriques de Darboux Barnabé Croizat, Laboratoire Paul Painlevé, Université Lille 1 & CNRS À l’occasion du centenaire de la mort de Gaston Darboux, l
From playlist Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - 17/11/2017

What is the difference between convex and concave polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
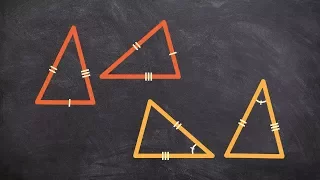
What is an Included Angle - Congruent Triangles
👉 Learn about the included angles of a triangle. An included angle of a triangle is the angle between two sides of a triangle. An included side of a triangle is the side between two angles. To show that two triangles are congruent by the side angle side (SAS) congruency theorem, we must s
From playlist Congruent Triangles

Generalization of an Integrability Theorem of Darboux and the Stable Configuration Condition In his monograph "Systèmes Orthogonaux" (Lecons sur les systèmes orthogonaux et les coordonnées curvilignes, Gauthier-Villars, Paris, 1910), Darboux stated three theorems providing local existence
From playlist DART X

What are the properties that make up a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - Hélène Gispert - 17/11/17
En partenariat avec le séminaire d’histoire des mathématiques de l’IHP Darboux c’est aussi le nom d’un journal : le Bulletin des sciences mathématiques (1869-1917) Hélène Gispert, GHDSO, Université Paris-Sud 11 À l’occasion du centenaire de la mort de Gaston Darboux, l’Institut Henri Poi
From playlist Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - 17/11/2017

What is the difference between concave and convex polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Brent Pym: Holomorphic Poisson structures - lecture 1
CIRM VIRTUAL EVENT Recorded during the research school "Geometry and Dynamics of Foliations " the April 28, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on
From playlist Virtual Conference

Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - David Rowe - 17/11/17
En partenariat avec le séminaire d’histoire des mathématiques de l’IHP Wartime Memories of Gaston Darboux in Göttingen David Rowe, Université de Mayence, Allemagne À l’occasion du centenaire de la mort de Gaston Darboux, l’Institut Henri Poincaré souhaite retracer la figure du géomètre s
From playlist Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - 17/11/2017

the Euler Poisson Darboux equation
In this video, I talk about one of my favorite math equations: the Euler-Poisson-Darboux equation. It's a PDE that is sort of a mean value formula for the wave equation, and will ultimately help us solve it. Enjoy! Partial Differential Equations playlist: https://www.youtube.com/playlist?
From playlist Partial Differential Equations

Identifying congruent parts between two polygons
👉 Learn how to solve with similar polygons. Two polygons are said to be similar if the corresponding angles are congruent (equal). When two polygons are similar the corresponding sides are proportional. Knowledge of the length of the sides or the proportion of the side lengths of one of th
From playlist Congruent Polygons

Nonlocality and degeneracy for the Hirota equation by Julia Cen
DATE: 04 June 2018 to 13 June 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore Non-Hermitian Physics-"Pseudo-Hermitian Hamiltonians in Quantum Physics (PHHQP) XVIII" is the 18th meeting in the series that is being held over the years in Quantum Physics. The scope of the program on Non-H
From playlist Non-Hermitian Physics - PHHQP XVIII

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Oleg Lazarev - Simplifying Weinstein Morse functions
June 29, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II