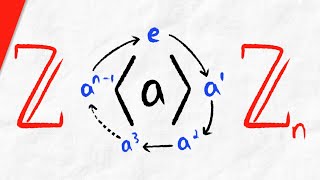
Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and a
From playlist Abstract Algebra

Cyclic Groups (Abstract Algebra)
Cyclic groups are the building blocks of abelian groups. There are finite and infinite cyclic groups. In this video we will define cyclic groups, give a list of all cyclic groups, talk about the name “cyclic,” and see why they are so essential in abstract algebra. Be sure to subscribe s
From playlist Abstract Algebra
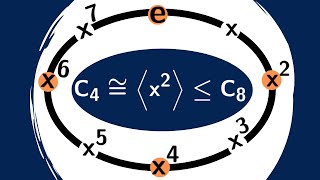
Abstract Algebra | Subgroups of Cyclic Groups
We prove that all subgroups of cyclic groups are themselves cyclic. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Direct Products of Finite Cyclic Groups Video 1
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Direct Products of Finite Cyclic Groups Video 1. How to determine if a direct product of finite cyclic groups is itself cyclic. This video has very easy examples.
From playlist Abstract Algebra
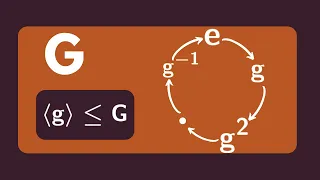
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Definition of a Cyclic Group with Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Cyclic Group with Examples
From playlist Abstract Algebra
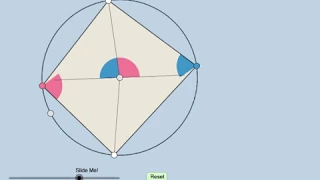
Cyclic Quadrilateral: Proof Hint!
Link: https://www.geogebra.org/m/KYdypjws
From playlist Geometry: Dynamic Interactives!

Cyclic groups are first and foremost, as the term implies, groups. What makes them cyclic is that at least on of the elements in the set that makes up the group under a specific binary operation can generate the group by performing the binary operation on itself. So, if a is an element o
From playlist Abstract algebra

Researchers Use Group Theory to Speed Up Algorithms — Introduction to Groups
This is the most information-dense introduction to group theory you'll see on this website. If you're a computer scientist like me and have always wondered what group theory is useful for and why it even exists and furthermore don't want to bother spending hours learning the basics, this i
From playlist Summer of Math Exposition 2 videos
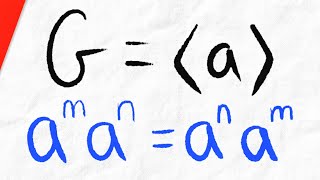
Every Cyclic Group is Abelian | Abstract Algebra
We prove every cyclic group is abelian by taking two arbitrary elements from an arbitrary cyclic group and showing they commute. Recall a cyclic group is entirely generated by all powers of a particular element. #abstractalgebra #grouptheory Cyclic Groups, Generators, and Cyclic Subgroup
From playlist Abstract Algebra

Maths for Programmers Tutorial - Full Course on Sets and Logic
Learn the maths and logic concepts that are important for programmers to understand. Shawn Grooms explains the following concepts: ⌨️ (00:00) Tips For Learning ⌨️ (01:32) What Is Discrete Mathematics? ⌨️ (03:45) Sets - What Is A Set? ⌨️ (06:22) Sets - Interval Notation & Common Sets ⌨️ (
From playlist Full Courses in One Video

RNT2.5.1. Euclidean Algorithm for Z/3[x]
Ring Theory: Let f(x)=x^5+2x^3+2x^2 + x+2 and g(x)=x^4+2x^3+2x^2 be polynomials over Z/3. Use the Euclidean algorithm to find gcd(f,g), find the prime factorizations of f and g, and find coefficients for Bezout's Identity in this case. We also find a field in which f(x) factors into l
From playlist Abstract Algebra
Introduction to number theory lecture 27. Groups and number theory
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We show how many of the theorems of number theory are special cases of theorems of groups t
From playlist Introduction to number theory (Berkeley Math 115)

One-Liner Competition 2012: Roman Osipov's Honorable Mention Entry
This video from Mathematica Experts Live: One-Liner Competition 2012 features Roman Osipov's Honorable Mention entry, an explorer of Venn diagrams for the complete set of Boolean functions of three variables. For more information about the event, please visit: http://www.wolfram.com/train
From playlist Mathematica Experts Live: One-Liner Competition 2012

Marcelo Frias: Relational tight field bounds for distributed analysis of programs
HYBRID EVENT Recorded during the meeting "19th International Conference on Relational and Algebraic Methods in Computer Science" the November 3, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other t
From playlist Virtual Conference

This lecture is part of an online graduate course on Galois theory. We prove the main theorem of Galois theory, given a bijection between subgroups of a Galois group and subextensions of a Galois extension. We illustrate it with the example of the splitting field of 4th roots of 2.
From playlist Galois theory

Lecture 17: Syntax, Part 7, and Semantics, Part 1
MIT 24.900 Introduction to Linguistics, Spring 2022 Instructor: Prof. Norvin W. Richards View the complete course: https://ocw.mit.edu/courses/24-900-introduction-to-linguistics-spring-2022/ YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP63BZGNOqrF2qf_yxOjuG35j This v
From playlist MIT 24.900 Introduction to Linguistics, Spring 2022

Vic Reiner, Lecture II - 11 February 2015
Vic Reiner (University of Minnesota) - Lecture II http://www.crm.sns.it/course/4036/ Many results in the combinatorics and invariant theory of reflection groups have q-analogues for the finite general linear groups GLn(Fq). These lectures will discuss several examples, and open questions
From playlist Algebraic topology, geometric and combinatorial group theory - 2015

If G is Cyclic so is G/H Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys If G is Cyclic so is G/H Proof. In this video we prove that if G is a cyclic group then the quotient group G/H is also cyclic. It turns out that if g is a generator for G, then Hg is a generator for G/H.
From playlist Abstract Algebra
