
Cyclic Groups (Abstract Algebra)
Cyclic groups are the building blocks of abelian groups. There are finite and infinite cyclic groups. In this video we will define cyclic groups, give a list of all cyclic groups, talk about the name “cyclic,” and see why they are so essential in abstract algebra. Be sure to subscribe s
From playlist Abstract Algebra
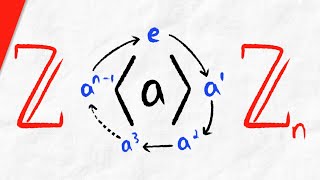
Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and a
From playlist Abstract Algebra

Direct Products of Finite Cyclic Groups Video 1
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Direct Products of Finite Cyclic Groups Video 1. How to determine if a direct product of finite cyclic groups is itself cyclic. This video has very easy examples.
From playlist Abstract Algebra
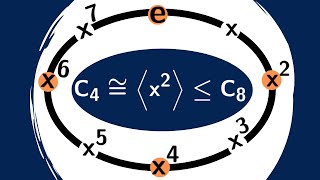
Abstract Algebra | Subgroups of Cyclic Groups
We prove that all subgroups of cyclic groups are themselves cyclic. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Definition of a Cyclic Group with Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Cyclic Group with Examples
From playlist Abstract Algebra

Cyclic groups are first and foremost, as the term implies, groups. What makes them cyclic is that at least on of the elements in the set that makes up the group under a specific binary operation can generate the group by performing the binary operation on itself. So, if a is an element o
From playlist Abstract algebra
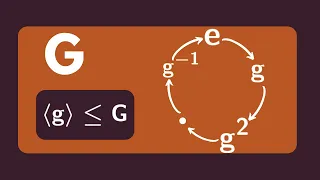
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Module Basics - Feb 17, 2021 - Rings and Modules
In this video we introduce basic notions like "cyclic" modules. This is the starting point for modules over PIDs.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Lecture 7: Hochschild homology in ∞-categories
In this video, we construct Hochschild homology in an arbitrary symmetric-monoidal ∞-category. The most important special case is the ∞-category of spectra, in which we get Topological Hochschild homology. Feel free to post comments and questions at our public forum at https://www.uni-mu
From playlist Topological Cyclic Homology

Michael Mandell: The strong Kunneth theorem for topological periodic cyclic homology
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Hesselholt has recently been advertising "topological periodic cyclic homology" (TP) as potentially filling some of the same roles for finite primes as periodic cyclic homology plays
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Visual Group Theory, Lecture 2.1: Cyclic and abelian groups
Visual Group Theory, Lecture 2.1: Cyclic and abelian groups In this lecture, we introduce two important families of groups: (1) "cyclic groups", which are those that can be generated by a single element, and (2) "abelian groups", which are those for which multiplication commutes. Addition
From playlist Visual Group Theory

Group theory 17: Finite abelian groups
This lecture is part of a mathematics course on group theory. It shows that every finitely generated abelian group is a sum of cyclic groups. Correction: At 9:22 the generators should be g, h+ng not g, g+nh
From playlist Group theory

CTNT 2020 - Heuristics for narrow class groups - Benjamin Breen
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos

Support Varieties for Modular Representations - Eric M. Friedlander
Members’ Seminar Topic: Support Varieties for Modular Representations Speaker: Eric M. Friedlander Affiliation: University of Southern California; Member, School of Mathematics Date: November 30, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Lecture 12: Topological periodic homology
In this video, we introduce another refinement of THH, the topological periodic homology TP. We see how it is an analogue of HP, how it is related to negative cyclic homology, and how to compute it for the field F_p. Feel free to post comments and questions at our public forum at https:/
From playlist Topological Cyclic Homology

The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: Workshop "Hermitian K-theory and trace methods"
From playlist HIM Lectures: Junior Trimester Program "Topology"

Ilya Dumanski - Schubert varieties in the Beilinson-Drinfeld Grassmannian
Ilya Dumanski (MIT) The Borel-Weil theorem states that the space of sections of a certain line bundle on the flag variety is isomorphic to the irreducible representation of the corresponding reductive group. The classical result of Demazure describes the restriction of sections to the Sch
From playlist Azat Miftakhov Days Against the War

F[x]-Module Derivation of Rational and Jordan Canonical Forms
Similar matrices isomorphism proof: https://youtu.be/-ligAAxFM8Y Every module is a direct sum of cyclic modules: https://youtu.be/gWIRI43h0ic Intro to F[x]-modules: https://youtu.be/H44q_Urmts0 The rational canonical form and Jordan normal form of a matrix are very important tools in li
From playlist Ring & Module Theory

Modular Forms | Modular Forms; Section 1 2
We define modular forms, and borrow an idea from representation theory to construct some examples. My Twitter: https://twitter.com/KristapsBalodi3 Fourier Theory (0:00) Definition of Modular Forms (8:02) In Search of Modularity (11:38) The Eisenstein Series (18:25)
From playlist Modular Forms
