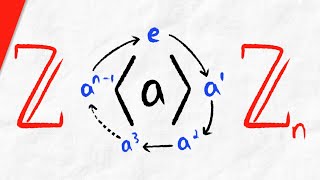
Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and a
From playlist Abstract Algebra

Cyclic Groups (Abstract Algebra)
Cyclic groups are the building blocks of abelian groups. There are finite and infinite cyclic groups. In this video we will define cyclic groups, give a list of all cyclic groups, talk about the name “cyclic,” and see why they are so essential in abstract algebra. Be sure to subscribe s
From playlist Abstract Algebra

Definition of a Cyclic Group with Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Cyclic Group with Examples
From playlist Abstract Algebra
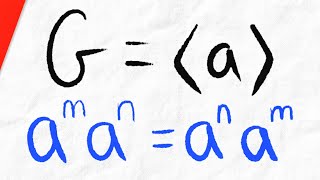
Every Cyclic Group is Abelian | Abstract Algebra
We prove every cyclic group is abelian by taking two arbitrary elements from an arbitrary cyclic group and showing they commute. Recall a cyclic group is entirely generated by all powers of a particular element. #abstractalgebra #grouptheory Cyclic Groups, Generators, and Cyclic Subgroup
From playlist Abstract Algebra

Cyclic groups are first and foremost, as the term implies, groups. What makes them cyclic is that at least on of the elements in the set that makes up the group under a specific binary operation can generate the group by performing the binary operation on itself. So, if a is an element o
From playlist Abstract algebra
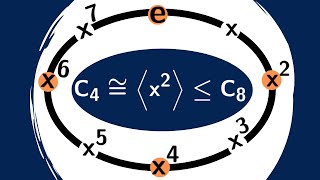
Abstract Algebra | Subgroups of Cyclic Groups
We prove that all subgroups of cyclic groups are themselves cyclic. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Direct Products of Finite Cyclic Groups Video 1
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Direct Products of Finite Cyclic Groups Video 1. How to determine if a direct product of finite cyclic groups is itself cyclic. This video has very easy examples.
From playlist Abstract Algebra
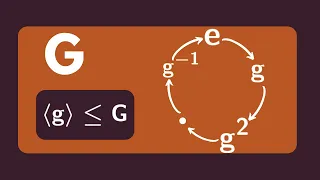
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Teena Gerhardt - 1/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Jonathan Belcher: Bridge cohomology-a generalization of Hochschild and cyclic cohomologies
Talk by Jonathan Belcher in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-... on August 12, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Henri Moscovici. Differentiable Characters and Hopf Cyclic Cohomology
Talk by Henri Moscovici in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/... on October 20, 2020.
From playlist Global Noncommutative Geometry Seminar (Europe)

Paolo Piazza: Proper actions of Lie groups and numeric invariants of Dirac operators
HYBRID EVENT shall explain how to define and investigate primary and secondary invariants of G-invariant Dirac operators on a cocompact G-proper manifold, with G a connected real reductive Lie group. This involves cyclic cohomology and Ktheory. After treating the case of cyclic cocycles a
From playlist Lie Theory and Generalizations

Masoud Khalkhali: Introduction to non commutative geometry 2
The lecture was held within the framework of the Hausdorff Trimester Program Non-commutative Geometry and its Applications. 8.9.2014
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Teena Gerhardt - 3/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Abstract Algebra - 4.1 Cyclic Groups and Their Properties (𝑎^𝑖=𝑎^𝑗)
We took a brief look at cyclic subgroups in our last chapter. In this chapter, we will review the definition of a cyclic group and look at a few examples to be sure we understand the concept. We then want to take a look at one of the two theorems we have related to cyclic groups and their
From playlist Abstract Algebra - Entire Course

Lecture 10: The circle action on THH
In this video we construct an action of the circle group S^1 = U(1) on the spectrum THH(R). We will see how this is the homotopical generalisation of the Connes operator. The key tool will be Connes' cyclic category. The speaker is of course Achim Krause and not Thomas Nikolaus as falsely
From playlist Topological Cyclic Homology
Sheagan John: Secondary higher invariants, and cyclic cohomology for groups of polynomial growth
Talk by Sheagan John in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on December 2, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Paolo Piazza: Surgery sequences and higher invariants of Dirac operators
Talk by Paolo Piazza in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on March 10, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

Structure of group rings and the group of units of integral group rings (Lecture 2) by Eric Jespers
PROGRAM : GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fun
From playlist Group Algebras, Representations And Computation

If G is Cyclic so is G/H Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys If G is Cyclic so is G/H Proof. In this video we prove that if G is a cyclic group then the quotient group G/H is also cyclic. It turns out that if g is a generator for G, then Hg is a generator for G/H.
From playlist Abstract Algebra