Coxeter element
In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter. (Wikipedia).
In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter. (Wikipedia).

Hankyung Ko: A singular Coxeter presentation
SMRI Algebra and Geometry Online Hankyung Ko (Uppsala University) Abstract: A Coxeter system is a presentation of a group by generators and a specific form of relations, namely the braid relations and the reflection relations. The Coxeter presentation leads to, among others, a similar pre
From playlist SMRI Algebra and Geometry Online

Group theory 23: Coxeter Todd algorithm
This lecture is part of an online mathematics course on group theory. It describes the Coxeter-Todd algorithm for coset enumeration, and gives some examples of it.
From playlist Group theory

Dipole Matrix Element Explained
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. In this video
From playlist Optoelectronic and Photonic Devices

Linear Algebra: Continuing with function properties of linear transformations, we recall the definition of an onto function and give a rule for onto linear transformations.
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

What Are Allotropes of Metalloids and Metals | Properties of Matter | Chemistry | FuseSchool
What Are Allotropes of Metalloids and Metals Learn the basics about allotropes of metalloids and metals, as a part of the overall properties of matter topic. An allotrope is basically a different form of the same element, each with distinct physical and chemical properties. For example
From playlist CHEMISTRY

Sets might contain an element that can be identified as an identity element under some binary operation. Performing the operation between the identity element and any arbitrary element in the set must result in the arbitrary element. An example is the identity element for the binary opera
From playlist Abstract algebra

Iron - Periodic Table of Videos
Iron and thermite. We have uploaded this video again higher resolution because the previous version was quite low quality. More links in description below ↓↓↓ Support Periodic Videos on Patreon: https://www.patreon.com/periodicvideos A video on every element: http://bit.ly/118elements M
From playlist All Chemical Elements in Order - Periodic Videos

Vic Reiner, Lecture III - 13 February 2015 (49)
Vic Reiner (University of Minnesota) - Lecture III http://www.crm.sns.it/course/4036/ Many results in the combinatorics and invariant theory of reflection groups have q-analogues for the finite general linear groups GLn(Fq). These lectures will discuss several examples, and open question
From playlist Vertex algebras, W-algebras, and applications - 2014-2015

Osamu Iyama: Preprojective algebras and Cluster categories
Abstract: The preprojective algebra P of a quiver Q has a family of ideals Iw parametrized by elements w in the Coxeter group W. For the factor algebra Pw=P/Iw, I will discuss tilting and cluster tilting theory for Cohen-Macaulay Pw-modules following works by Buan-I-Reiten-Scott, Amiot-Rei
From playlist Combinatorics
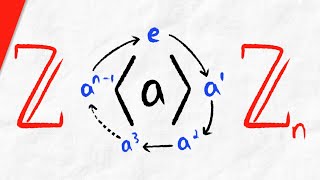
Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and a
From playlist Abstract Algebra

Homological Algebra(Homo Alg) 5 by Graham Ellis
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Representation Theory(Repn Th) 5 by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods
Invariants of Graphs, Their Associated Clique Complexes and Right-Angled... - Michael Davis
Michael Davis The Ohio State University; Member, School of Mathematics October 19, 2010 Associated to any simplicial graph there is a right-angled Coxeter group. Invariants of the Coxeter group such as its growth series or its weighted L^2 Betti numbers can be computed from the graph's cli
From playlist Mathematics

Olga Varghese: Automorphism groups of Coxeter groups do not have Kazhdan's property (T)
CIRM VIRTUAL EVENT Recorded during the meeting "Virtual Geometric Group Theory conference " the May 27, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIR
From playlist Virtual Conference

Singular Hodge theory of matroids - Jacob Matherne
Joint IAS/Princeton University Algebraic Geometry Seminar Topic: Singular Hodge theory of matroids Speaker: Jacob Matherne Affiliation: Member, School of Mathematics Date: March 25, 2019 For more video please visit http://video.ias.edu
From playlist Joint IAS/PU Algebraic Geometry
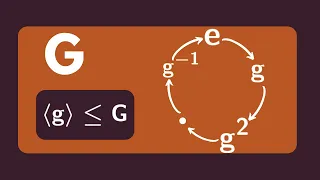
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Petra Schwer: Studying affine Deligne Lusztig varieties via folded galleries in buildings
Abstract: We present a new approach to affine Deligne Lusztig varieties which allows us to study the so called "non-basic" case in a type free manner. The central idea is to translate the question of non-emptiness and the computation of the dimensions of these varieties into geometric ques
From playlist Algebra

Diophantine analysis in thin orbits - Alex Kontorovich
Special Seminar Topic: Diophantine analysis in thin orbits Speaker: Alex Kontorovich Affiliation: Rutgers University; von Neumann Fellow, School of Mathematics Date: December 8, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra