
Conceptual Questions about Correlation
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Conceptual Questions about Correlation
From playlist Statistics

Intro to the Correlation Coefficient
Brief intro to the correlation coefficient. What it means to have negative correlation, positive correlation or zero correlation. Pearson's, sample and population formulas.
From playlist Correlation

Covariance (8 of 17) What is the Correlation Coefficient?
Visit http://ilectureonline.com for more math and science lectures! To donate:a http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn what is and how to find the correlation coefficient of 2 data sets and see how it corresponds to the graph of the data
From playlist COVARIANCE AND VARIANCE

Limits of correlation (applied)
Correlation is a standardized covariance (i.e., translated into unit-less form with volatilities). It cannot be used alone: (i) it can be "distorted" by low volatilities, and (ii) it does not give information revealed by the scatter (in this example, both hedge fund series are similarly co
From playlist Statistics: Introduction

Covariance Definition and Example
What is covariance? How do I find it? Step by step example of a solved covariance problem for a sample, along with an explanation of what the results mean and how it compares to correlation. 00:00 Overview 03:01 Positive, Negative, Zero Correlation 03:19 Covariance for a Sample Example
From playlist Correlation

This video explains how to find the correlation coefficient which describes the strength of the linear relationship between two variables x and y. My Website: https://www.video-tutor.net Patreon: https://www.patreon.com/MathScienceTutor Amazon Store: https://www.amazon.com/shop/theorga
From playlist Statistics

Covariance (1 of 17) What is Covariance? in Relation to Variance and Correlation
Visit http://ilectureonline.com for more math and science lectures! To donate:a http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn the difference between the variance and the covariance. A variance (s^2) is a measure of how spread out the numbers of
From playlist COVARIANCE AND VARIANCE

Covariance (12 of 17) Covariance Matrix wth 3 Data Sets and Correlation Coefficients
Visit http://ilectureonline.com for more math and science lectures! To donate:a http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will find the correlation coefficients of the 3 data sets form the previous 2 videos. Next video in this series can be seen at:
From playlist COVARIANCE AND VARIANCE

Correlation induced metallic, half-metallic and superconducting by H. R. Krishnamurthy
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019

Tunable gaps and bandwidths in twisted double bilayer graphene system by Mandar Deshmukh
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019

André Marie Tremblay - High temperature superconductors: Where is the mystery?
PROGRAM: STRONGLY CORRELATED SYSTEMS: FROM MODELS TO MATERIALS DATES: Monday 06 Jan, 2014 - Friday 17 Jan, 2014 VENUE: Department of Physics, IISc Campus, Bangalore PROGRAM LINK : http://www.icts.res.in/program/MTM2014 The realistic description of materials with strong electron-electro
From playlist Strongly correlated systems: From models to materials

Quantum Transport, Lecture 13: Superconductivity
Instructor: Sergey Frolov, University of Pittsburgh, Spring 2013 http://sergeyfrolov.wordpress.com/ Summary: basics of superconductivity, Cooper pairing, energy gap, Andreev reflection. Quantum Transport course development supported in part by the National Science Foundation under grant DM
From playlist Quantum Transport

AQC 2016 - Inhomogeneous Quasi-adiabatic Driving of Quantum Critical Dynamics
A Google TechTalk, June 27, 2016, presented by Masoud Mohseni (Google) ABSTRACT: We introduce an inhomogeneous protocol to drive a weakly disordered quantum spin chain quasi-adiabatically across a quantum phase transition and minimize the residual energy of the final state. The number of
From playlist Adiabatic Quantum Computing Conference 2016

Lec 16 | MIT 5.74 Introductory Quantum Mechanics II, Spring 2009
Lecture 16: Characterizing Fluctuations View the complete course: http://ocw.mit.edu/5-74S09 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 5.74 Introductory Quantum Mechanics II, Spring 2009

Computer Science/Discrete Mathematics Seminar I Topic: MIP* = RE Speaker: Henry Yuen Affiliation: University of Toronto Date: February 03, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Didier POILBLANC - Investigation of the chiral antiferromagnetic Heisenberg model using PEPS
https://indico.math.cnrs.fr/event/2435/
From playlist Workshop “Hamiltonian methods in strongly coupled Quantum Field Theory”

Anna Keselman: "Spectral Signatures of Quasiparticle Interactions in Antiferromagnets"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "Spectral Signatures of Quasiparticle Interactions in Antiferromagnets" Anna Keselman - Kavli Institute for Theoretical Physics Abstract: Elementary excitat
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021
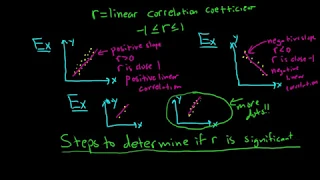
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Correlation
From playlist Statistics

Continuous Mott transitions in a model Hamiltonian system by N S Vidhyadhiraja
29 May 2017 to 02 June 2017 VENUE: Ramanujan Lecture Hall, ICTS Bangalore This program aims to bring together people working on classical and quantum systems with disorder and interactions. The extensive exploration, through experiments, simulations and model calculations, of growing cor
From playlist Correlation and Disorder in Classical and Quantum Systems
