
Continuity: Definitions & basic concept
More resources available at www.misterwootube.com
From playlist Introduction to Differentiation

Introduction to Discrete and Continuous Functions
This video defines and provides examples of discrete and continuous functions.
From playlist Introduction to Functions: Function Basics

(New Version Available) Inverse Functions
New Version: https://youtu.be/q6y0ToEhT1E Define an inverse function. Determine if a function as an inverse function. Determine inverse functions. http://mathispower4u.wordpress.com/
From playlist Exponential and Logarithmic Expressions and Equations

Determine if a Relation is a Function
http://mathispower4u.wordpress.com/
From playlist Intro to Functions

Math 131 092816 Continuity; Continuity and Compactness
Review definition of limit. Definition of continuity at a point; remark about isolated points; connection with limits. Composition of continuous functions. Alternate characterization of continuous functions (topological definition). Continuity and compactness: continuous image of a com
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

What are bounded functions and how do you determine the boundness
👉 Learn about the characteristics of a function. Given a function, we can determine the characteristics of the function's graph. We can determine the end behavior of the graph of the function (rises or falls left and rises or falls right). We can determine the number of zeros of the functi
From playlist Characteristics of Functions
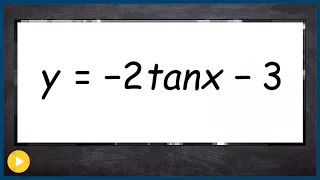
Explaining if the tangent function is a continuous function or not
👉 Learn all about the Limit. In this playlist, we will explore how to evaluate the limit of an equation, piecewise function, table and graph. We will explore continuity as well as discontinuities such as holes, asymptotes and jumps and how they relate to the limit. We will evaluate the g
From playlist Is the Functions Continuous or Not?

Functions of equations - IS IT A FUNCTION
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

This video explains what a mathematical function is and how it defines a relationship between two sets, the domain and the range. It also introduces three important categories of function: injective, surjective and bijective.
From playlist Foundational Math

Introduction to Lattice Field Theory by Anna Hasenfratz
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Nathan Seiberg - Quantum Field Theory of Exotic Systems - IPAM at UCLA
Recorded 03 September 2021. Nathan Seiberg of the Institute for Advanced Study presents "Quantum Field Theory of Exotic Systems" at IPAM's Graduate Summer School: Mathematics of Topological Phases of Matter. This was Nathan's second presentation of the week. Abstract: Until recently, it wa
From playlist Graduate Summer School 2021: Mathematics of Topological Phases of Matter

Robert Batterman - Mesoscale Models and Many-Body Systems - IPAM at UCLA
Recorded 17 February 2022. Robert Batterman of the University of Pittsburgh presents "Mesoscale Models and Many-Body Systems" at IPAM's Mathematics of Collective Intelligence Workshop. Abstract: Many-body systems often display different behaviors at different scales. The behavior of a flui
From playlist Workshop: Mathematics of Collective Intelligence - Feb. 15 - 19, 2022.

Studying thermal QCD matter on the lattice (LQCD1 - Lecture 2) by Peter Petreczky
PROGRAM THE MYRIAD COLORFUL WAYS OF UNDERSTANDING EXTREME QCD MATTER ORGANIZERS: Ayan Mukhopadhyay, Sayantan Sharma and Ravindran V DATE: 01 April 2019 to 17 April 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Strongly interacting phases of QCD matter at extreme temperature and
From playlist The Myriad Colorful Ways of Understanding Extreme QCD Matter 2019

Should the power class of any non-empty set even be a set? It's not in constructive Zermelo-Fraenkel, but once you add the Axiom of Choice you end up in ZFC where you have to assign it a cardinal number. But then, well-orderings on something like the reals provably exist that are not descr
From playlist Logic

Nathan Seiberg - Quantum Field Theory of Exotic Systems - IPAM at UCLA
Recorded 30 August 2021. Nathan Seiberg of the Institute for Advanced Study presents "Quantum Field Theory of Exotic Systems" at IPAM's Graduate Summer School: Mathematics of Topological Phases of Matter. This is the first of Nathan's two presentations. Abstract: Until recently, it was wid
From playlist Graduate Summer School 2021: Mathematics of Topological Phases of Matter

An Alternative Lattice Field Theory Formulation Inspired by Noboru Kawamoto
Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography DATE:27 January 2018 to 03 February 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The program "Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography" aims to
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography

Nathan Seiberg - Exotic Field Theories: Lifshitz Theory, Tensor Gauge Theory, and Fractons
Over the past few years, many exotic lattice systems with peculiar properties were found. Some of their peculiarities include particles with restricted mobility, large ground-state degeneracy, and long-distance sensitivity to short-distance details. Consequently, these theories do not have
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Frank Verstraete: "Algorithms for continuous matrix product states"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "Algorithms for continuous matrix product states" Frank Verstraete - Ghent University Abstract: This talk will give an overview of state of the art algorith
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021
Does Infinite Cardinal Arithmetic Resemble Number Theory? - Menachem Kojman
Menachem Kojman Ben-Gurion University of the Negev; Member, School of Mathematics February 28, 2011 I will survey the development of modern infinite cardinal arithmetic, focusing mainly on S. Shelah's algebraic pcf theory, which was developed in the 1990s to provide upper bounds in infinit
From playlist Mathematics

Determine if the equation represents a function
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function