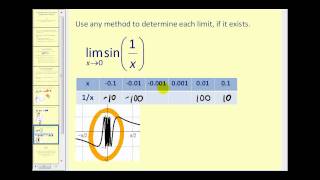
Determining Limits of Trigonometric Functions
An introductory video on determining limits of trigonometric functions. http://mathispower4u.wordpress.com/
From playlist Limits

Rigidity of the hexagonal triangulation of the plane and its applications - Feng Luo
Feng Luo, Rutgers October 5, 2015 http://www.math.ias.edu/wgso3m/agenda 015-2016 Monday, October 5, 2015 - 08:00 to Friday, October 9, 2015 - 12:00 This workshop is part of the topical program "Geometric Structures on 3-Manifolds" which will take place during the 2015-2016 academic year
From playlist Workshop on Geometric Structures on 3-Manifolds

Computing Delaunay complex: Lifting to a paraboloid [Ondřej Draganov]
Short visual explanation of a construction of Delaunay complex via lifting to a paraboloid and projecting. This construction reduces the problem of finding the Delaunay complex of a d-dimensional point cloud to finding a lower convex hull of a (d+1)-dimensional point cloud. This video is
From playlist Tutorial-a-thon 2021 Fall

How far is it from everywhere to somewhere?
Computing the Euclidean Distance Transform on a regular grid. A fundamental operation in image processing, used as part of separating objects, finding best matches, finding sizes of objects, and so on. The algorithm presented here is described in: J. Wang and Ying Tan, Efficient Euclide
From playlist Summer of Math Exposition Youtube Videos

Navigating Intrinsic Triangulations - SIGGRAPH 2019
Navigating Intrinsic Triangulations. Nicholas Sharp, Yousuf Soliman, and Keenan Crane. ACM Trans. on Graph. (2019) http://www.cs.cmu.edu/~kmcrane/Projects/NavigatingIntrinsicTriangulations/paper.pdf We present a data structure that makes it easy to run a large class of algorithms from co
From playlist Research

Voronoi diagram, Delaunay and Alpha complexes: A Visual Intro [Ondřej Draganov]
Introductory tutorial bringing visual intuition into definitions of three basic concepts used in TDA – Voronoi diagrams, Delaunay complexes and Alpha complexes / Alpha filtration. In this video I show how to get from a two-dimensional point-cloud to each of those objects, describe several
From playlist Tutorial-a-thon 2021 Spring

Protein Folding Characterization via Persistent Homology - Marcio Gameiro
Workshop on Topology: Identifying Order in Complex Systems Topic: Protein Folding Characterization via Persistent Homology Speaker: Marcio Gameiro Affiliation: University of Sao Paolo Date: April 7, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Evaluate the limit with tangent
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Use limit laws and special trig limits to evaluate
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

A Laplacian for Nonmanifold Triangle Meshes - SGP 2020
Authors: Nicholas Sharp and Keenan Crane presented at SGP 2020 https://sgp2020.sites.uu.nl https://github.com/nmwsharp/nonmanifold-laplacian Abstract: We describe a discrete Laplacian suitable for any triangle mesh, including those that are nonmanifold or nonorientable (with or without b
From playlist Research

SHM - 12/05/17 - La cosmographie dans l'enseignement secondaire (...) - Colette Le Lay
Assumer ou contourner la technicité mathématique dans les apprentissages de la cosmographie (séance préparée par Catherine Radtka et Norbert Verdier) 14 h -16h : - Colette Le Lay (Centre François Viète, Université de Nantes) : « La cosmographie dans l'enseignement secondaire au XIXe si
From playlist Séminaire d'Histoire des Mathématiques
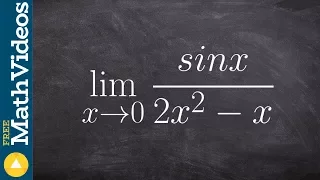
Evaluate special trigonometric limits using algebra
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Evaluating the limit using properties of limits and special trig limits
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Thomas Fernique - Maximally Dense Sphere Packings
It is well known that to cover the greatest proportion of the Euclidean plane with identical disks, we have to center these disks in a triangular grid. This problem can be generalized in two directions: in higher dimensions or with different sizes of disks. The first direction has been the
From playlist Combinatorics and Arithmetic for Physics: special days

How to use special trig limits to evaluate the limit
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig
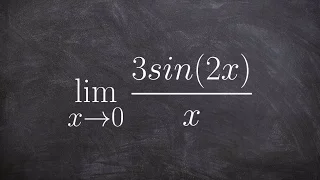
Learn how to use special trig limits to evaluate
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Evaluating the limit using special trig limits
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Using trig limits to evaluate the limit
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

S.Schleimer - An introduction to veering triangulations
Singular euclidean structures on surfaces are a key tool in the study of the mapping class group, of Teichmüller space, and of kleinian three-manifolds. François Guéritaud, while studying work of Ian Agol, gave a powerful technique for turning a singular euclidean structure (on a surface)
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Evaluate the limit using special trigonometric limit of cosine
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig