
Natural Deductive Logic: RULES #1 (R, &E, &I, MP, CP) - Logic
In this video we introduce natural deductive proofs and our first set of rules of inference: Reiteration, conjunction elimination, conjunction introduction, modus ponens (conditional elimination), and conditional proof (conditional introduction). 0:00 [Proofs in Propositional Logic] 1:51
From playlist Logic in Philosophy and Mathematics

Logic 4: Natural Deduction with Logical Axioms — Tutorial 4/4
In this four-part series we explore propositional logic, Karnaugh maps, implications and fallacies, predicate logic, existential and universal quantifiers and finally natural deduction. Become a member: https://youtube.com/Bisqwit/join My links: Twitter: https://twitter.com/RealBisqwit L
From playlist Logic Tutorial
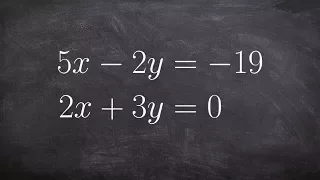
How to Use Elimination to Solve a System of Equations
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Hard

Foundations - Seminar 12 - Gödel's incompleteness theorem Part 4
Billy Price and Will Troiani present a series of seminars on foundations of mathematics. In this seminar Will Troiani continues with the proof of Gödel's incompleteness theorem, by proving that general recursive functions are representable. You can join this seminar from anywhere, on any
From playlist Foundations seminar

Applying Elimination to Solve a System of Equations with One Solution
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Two Exercises in Natural Deductive Logic: RULES #1 (R, &E, &I, MP, CP) - Logic
We do two more natural deductive proofs using the rules introduced in the last video. They are listed below. 0:00 [Intro] 0:31 [Question #1] 5:27 [Question #2] 9:45 [The Takeaway] Follow along in the Logic playlist: https://www.youtube.com/playlist?list=PLDDGPdw7e6AhsNuxXP3D-45Is96L8sdSG
From playlist Logic in Philosophy and Mathematics

Solving a system of equations with infinite many solutions
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Nexus trimester - Yitong Yin (Nanjing University)
Rectangle inequalities for data structure lower bounds Yitong Yin (Nanjing University) February 23, 2016 Abstract: The richness lemma is a classic rectangle-based technique for asymmetric communication complexity and cell-probe lower bounds. The technique was enhanced by the Patrascu-Thoru
From playlist Nexus Trimester - 2016 - Fundamental Inequalities and Lower Bounds Theme
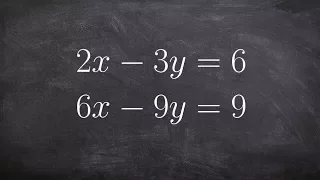
Labeling a System by Solving Using Elimination Method
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Stepan Kuznetsov: Relational models for the Lambek calculus with intersection and unit
HYBRID EVENT Recorded during the meeting "19th International Conference on Relational and Algebraic Methods in Computer Science" the November 5, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other t
From playlist Logic and Foundations
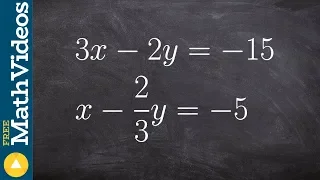
Solve a system of equation when they are the same line
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium
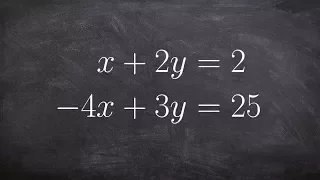
Using a Multiplier to Solve the System of Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Natural Deductive Logic: RULES #2 (vI, vE, DN, RAA) - Logic
In this video on #Logic, we learn four more rules for natural deductive proofs. We learn disjunction introduction, disjunction elimination, double negation, and reductio ad absurdum (negation introductions, or proof by contradiction). Then we do two example proofs. #PropositionalLogic #Lo
From playlist Logic in Philosophy and Mathematics

How to Solve a System of Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Enregistré pendant la session « Algorithmique et programmation » le 8 mai 2018 au Centre International de Rencontres Mathématiques (Marseille, France) Réalisation: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Lib
From playlist Mathematical Aspects of Computer Science

Natural Deductive Logic: RULES #3 (=I, =E) - Logic
In this video on #Logic, we learn our last two rules for natural deductive proofs. We learn biconditional introduction and biconditional elimination. Then we do a few example proofs. #PropositionalLogic #LogicProofs 0:00 [Rule: Biconditional Introduction] 1:47 [Rule: Biconditional Elimin
From playlist Logic in Philosophy and Mathematics

The Nature of Causation: The Regularity Theory
What is causation? In this first lecture in this series on the nature of causation, Marianne Talbot discusses Hume's famous account of causation, which is a version of the so-called regularity theory. We have causal theories of reference, perception, knowledge, content and numerous other
From playlist The Nature of Causation

Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium
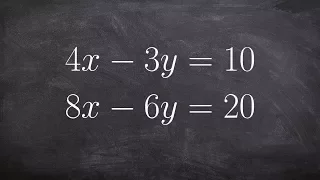
Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium