
Learn how to classify conic sections
Learn how to classify conic sections. A conic section is a figure formed by the intersection of a plane and a cone. A conic section may be a circle, an ellipse, a parabola, or a hyperbola. The general equation of a conic section is given by Ax^2 + By^2 + Cx + Dy + E = 0. When given the ge
From playlist The Hyperbola in Conic Sections

Learn how to classify conic sections
Learn how to classify conic sections. A conic section is a figure formed by the intersection of a plane and a cone. A conic section may be a circle, an ellipse, a parabola, or a hyperbola. The general equation of a conic section is given by Ax^2 + By^2 + Cx + Dy + E = 0. When given the ge
From playlist The Hyperbola in Conic Sections

Steps to classify conic sections
Learn how to classify conic sections. A conic section is a figure formed by the intersection of a plane and a cone. A conic section may be a circle, an ellipse, a parabola, or a hyperbola. The general equation of a conic section is given by Ax^2 + By^2 + Cx + Dy + E = 0. When given the ge
From playlist The Hyperbola in Conic Sections

How to determine if an equation is a parabloa, circle, ellipse or hyperbola, conics
http://www.freemathvideos.com In this video series I will show you how to write the equation and graph hyperbolas. Hyperbolas on a graph represent two parabolas facing away from each other but the definition of a hyperbola is the difference between the distance of a set of points and the
From playlist How to Classify Conic Sections #Conics
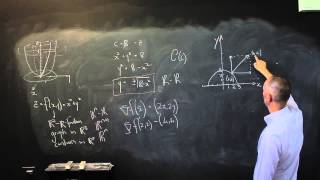
11_6_1 Contours and Tangents to Contours Part 1
A contour is simply the intersection of the curve of a function and a plane or hyperplane at a specific level. The gradient of the original function is a vector perpendicular to the tangent of the contour at a point on the contour.
From playlist Advanced Calculus / Multivariable Calculus

Tangent conics and tangent quadrics | Differential Geometry 5 | NJ Wildberger
In this video we further develop and extend Lagrange's algebraic approach to the differential calculus. We show how to associate to a polynomial function y=p(x) at a point x=r not just a tangent line, but also a tangent conic, a tangent cubic and so on. Only elementary high school manipul
From playlist Differential Geometry

What is the definition of a parabola
Learn all about parabolas in conic sections. We will discover the basic definitions such as the vertex, focus, directrix, and axis of symmetry. We will also take a look a basic processes such as graphing, writing the equation and identifying a parabolas parts when given an equation in sta
From playlist Learn all about Parabolas #Conics

What is the definition of a parabola for CONIC sections
Learn all about parabolas in conic sections. We will discover the basic definitions such as the vertex, focus, directrix, and axis of symmetry. We will also take a look a basic processes such as graphing, writing the equation and identifying a parabolas parts when given an equation in sta
From playlist Learn all about Parabolas #Conics

What are the basic characteristics of a parabola for conic sections
Learn all about parabolas in conic sections. We will discover the basic definitions such as the vertex, focus, directrix, and axis of symmetry. We will also take a look a basic processes such as graphing, writing the equation and identifying a parabolas parts when given an equation in sta
From playlist Learn all about Parabolas #Conics

Mordell Weil rank jumps and the Hilbert property - Salgado - Workshop 1 - CEB T2 2019
Cecília Salgado (UFRJ) / 21.05.2019 Mordell Weil rank jumps and the Hilbert property We study rank jumps of the Mordell-Weil groups of the fibres of elliptic surfaces. I will discuss the cases for which we show that the set for which the rank jumps is not thin. This is a work in progres
From playlist 2019 - T2 - Reinventing rational points

Lorenzo Foscolo: ALC manifolds with exceptional holonomy
We will describe the construction of complete non-compact Ricci-flat manifolds of dimension 7 and 8 with holonomy $G_{2}$ and Spin(7) respectively. The examples we consider all have non-maximal volume growth and an asymptotic geometry, so-called ALC geometry, that generalises to higher dim
From playlist Geometry

Complex surfaces 3: Rational surfaces
We give an informal survey of some complex rational surfaces. We first lift a few examples: hypersurfaces of degree at most 3, and the Hirzebruch surfaces which are P1 bundles over P1. Then we discuss the surfaces obtained by blowing up points in the plane in more detail. We sketch how to
From playlist Algebraic geometry: extra topics

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 1/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 4/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Takeshi Saito - Micro support of a constructible sheaf in mixed characteristic
Correction: The affiliation of Lei Fu is Tsinghua University. One of the obstacles in the definition of the singular support of a constructible sheaf in mixed characteristic is the absence of the cotangent bundle. We define a ‘Frobenius pull-back’ of the cotangent bundle restricted on the
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

Bjorn Poonen - Cohomological Obstructions to Rational Points [2008]
Cohomological Obstructions to Rational Points. CMI/MSRI Workshop: Modular Forms And Arithmetic June 28, 2008 - July 02, 2008 June 30, 2008 (10:30 AM PDT - 11:30 AM PDT) Speaker(s): Bjorn Poonen (Massachusetts Institute of Technology) Location: MSRI: Simons Auditorium http://www.msri.org
From playlist Number Theory

Hyperbola with Foci (-3, 0), (1, 0) and Vertices (-2, 0), (0, 0)
We find the equation of the hyperbola with foci (-3, 0), (1, 0), and vertices (-2 0), (0,0). Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys
From playlist Conics

Modular spectral covers and Hecke eigensheaves on interesections (Lecture 2) by Tony Pantev
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

