
In this video, we'll learn how to view a complex number as a 2x2 matrix with a special form. We'll also see that there is a matrix version for the number 1 and a matrix representation for the imaginary unit, i. Furthermore, the matrix representation for i has the defining feature of the im
From playlist Complex Numbers

Complex Matrices ( An intuitive visualization )
Complex Matrices are not given enough credit for what they do and even when they are used its often introduced as an foreign entity. This video was made to shed light on such a misinterpreted topic. Timestamps 00:00 - Introduction 00:11 - Matrix 00:45 - Complex Number 02:50 - Complex Ma
From playlist Summer of Math Exposition Youtube Videos

Complex Numbers as Points (1 of 4: Geometric Meaning of Addition)
More resources available at www.misterwootube.com
From playlist Complex Numbers

Introduction to Complex Numbers (Free Ebook)
http://bookboon.com/en/introduction-to-complex-numbers-ebook This free ebook makes learning "complex" numbers easy through an interactive, fun and personalized approach. Features include: live YouTube video streams and closed captions that translate to 90 languages! Complex numbers "break
From playlist Intro to Complex Numbers

Today, we take a look at how we can represent complex numbers in matrix form.
From playlist Complex Analysis

What is the complex conjugate?
What is the complex conjugate of a complex number? Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook
From playlist Intro to Complex Numbers

ComplexMultiplication 1/3 - i/3
From playlist Complex Multiplication

Complex Power: (1 + i sqrt(3))^3
From playlist Complex Multiplication

Representation theory: The Schur indicator
This is about the Schur indicator of a complex representation. It can be used to check whether an irreducible representation has in invariant bilinear form, and if so whether the form is symmetric or antisymmetric. As examples we check which representations of the dihedral group D8, the
From playlist Representation theory

Supercuspidal representations of GL(n) over a p-adic field distinguished... by Vincent Sécherre
PROGRAM : ALGEBRAIC AND ANALYTIC ASPECTS OF AUTOMORPHIC FORMS ORGANIZERS : Anilatmaja Aryasomayajula, Venketasubramanian C G, Jurg Kramer, Dipendra Prasad, Anandavardhanan U. K. and Anna von Pippich DATE & TIME : 25 February 2019 to 07 March 2019 VENUE : Madhava Lecture Hall, ICTS Banga
From playlist Algebraic and Analytic Aspects of Automorphic Forms 2019
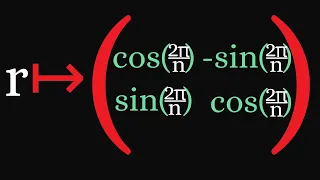
Representations of Finite Groups | A few more common examples.
We present a few more common examples of representations of finite groups. These include cyclic groups, dihedral groups, the quaternions, and the symmetric group. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net R
From playlist Representations of Finite Groups

Kevin Buzzard (lecture 16/20) Automorphic Forms And The Langlands Program [2017]
Full course playlist: https://www.youtube.com/playlist?list=PLhsb6tmzSpiysoRR0bZozub-MM0k3mdFR http://wwwf.imperial.ac.uk/~buzzard/MSRI/ Summer Graduate School Automorphic Forms and the Langlands Program July 24, 2017 - August 04, 2017 Kevin Buzzard (Imperial College, London) https://w
From playlist MSRI Summer School: Automorphic Forms And The Langlands Program, by Kevin Buzzard [2017]

Representation theory: Abelian groups
This lecture discusses the complex representations of finite abelian groups. We show that any group is iomorphic to its dual (the group of 1-dimensional representations, and isomorphic to its double dual in a canonical way (Pontryagin duality). We check the orthogonality relations for the
From playlist Representation theory

Vincent Sécherre - Congruence properties of endoclasses...
Congruence properties of endoclasses and the local Jacquet-Langlands correspondence Consider the local Jacquet-Langlands correspondence between the discrete series representations of a general linear group H over some non-Archimedean locally compact field F and those of an inner form G of
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

[Lesson 28] QED Prerequisites Scattering 5
In this lesson we discover the integral representation of the Hankel function. We are doing this in preparation of executing the Method of Steepest Descents/Saddle Point Method to determine its asymptotic form. Please consider supporting this channel on Patreon: https://www.patreon.com/X
From playlist QED- Prerequisite Topics

Representations of Finite Groups | Definitions and simple examples.
We define the notion of a representation of a group on a finite dimensional complex vector space. We also explore one and two dimensional representations of the cyclic group Zn. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.mich
From playlist Representations of Finite Groups

Graphs in the Complex Plane (1 of 4: Introductory Examples)
More resources available at www.misterwootube.com
From playlist Complex Numbers

Higgs bundles and higher Teichmüller components (Lecture 1) by Oscar Garcia
DISCUSSION MEETING : MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE : 10 February 2020 to 14 February 2020 VENUE : Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classif
From playlist Moduli Of Bundles And Related Structures 2020

