Complement (complexity)

Computational complexity theory

In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement problem. For example, one important problem is whether a number is a prime number. Its complement is to determine whether a number is a composite number (a number which is not prime). Here the domain of the complement is the set of all integers exceeding one. There is a Turing reduction from every problem to its complement problem. The complement operation is an involution, meaning it "undoes itself", or the complement of the complement is the original problem. One can generalize this to the complement of a complexity class, called the complement class, which is the set of complements of every problem in the class. If a class is called C, its complement is conventionally labelled co-C. Notice that this is not the complement of the complexity class itself as a set of problems, which would contain a great deal more problems. A class is said to be closed under complement if the complement of any problem in the class is still in the class. Because there are Turing reductions from every problem to its complement, any class which is closed under Turing reductions is closed under complement. Any class which is closed under complement is equal to its complement class. However, under many-one reductions, many important classes, especially NP, are believed to be distinct from their complement classes (although this has not been proven). The closure of any complexity class under Turing reductions is a superset of that class which is closed under complement. The closure under complement is the smallest such class. If a class is intersected with its complement, we obtain a (possibly empty) subset which is closed under complement. Every deterministic complexity class (DSPACE(f(n)), DTIME(f(n)) for all f(n)) is closed under complement, because one can simply add a last step to the algorithm which reverses the answer. This doesn't work for nondeterministic complexity classes, because if there exist both computation paths which accept and paths which reject, and all the paths reverse their answer, there will still be paths which accept and paths which reject — consequently, the machine accepts in both cases. Similarly, probabilistic classes such as BPP, ZPP, BQP or PP which are defined symmetrically with regards to their yes and no instances are closed under complement. In contrast, classes such as RP and co-RP define their probabilities with one-sided error, and so are not (currently known to be) closed under complement. Some of the most surprising complexity results shown to date showed that the complexity classes NL and SL are in fact closed under complement, whereas before it was widely believed they were not (see Immerman–Szelepcsényi theorem). The latter has become less surprising now that we know SL equals L, which is a deterministic class. Every class which is low for itself is closed under complement. (Wikipedia).

Complex Power: (1+i)^8

From playlist Complex Multiplication

Ex: Evaluate a Combination and a Permutation - (n,r)

This video explains how to evaluate a combination and a permutation with the same value of n and r. Site: http://mathispower4u.com

From playlist Permutations and Combinations

B22 Introduction to Substitutions

An overview of the three type of substitutions as a new method of solving linear, exact, and "almost" separable differential equations.

From playlist Differential Equations

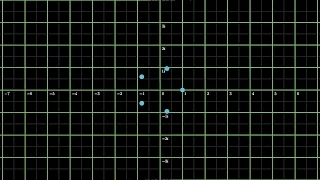
Complex Power: (cos(72) + isin(72))^5

From playlist Complex Multiplication

ComplexMultiplication 1/3 - i/3

From playlist Complex Multiplication

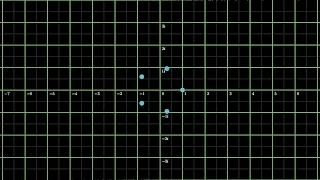
Complex Magnitude Equation with Geometric Interpretation

A response to Fematika's video about complex loci.

From playlist Challenge Problems

Complex Power: (cos(144) + isin(144))^5

From playlist Complex Multiplication

Complex Power: (cos(-72) + isin(-72))^5

From playlist Complex Multiplication

Complex Numbers as Points (1 of 4: Geometric Meaning of Addition)

More resources available at www.misterwootube.com

From playlist Complex Numbers

The Complement System: Classical, Lectin, and Alternative Pathways

We are learning about the features of innate immunity, and one that is often overlooked is the complement system. This is a very complicated ensemble of proteins circulating in the bloodstream that activate each other in a specific sequence that results in immune system engagement to kill

From playlist Immunology

Tiny Bombs in your Blood - The Complement System

Sources: https://sites.google.com/view/sources-complement-system One of the key players of our immune system is the complement system. An army of millions and trillions of tiny bombs, which work together in a complex and elegant dance to stop intruders in your body. OUR CHANNELS ▀▀▀▀▀▀▀

From playlist Medicine & Biology

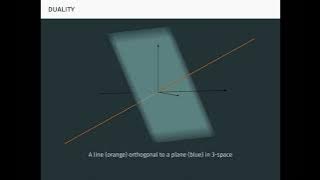
Duality in Linear Algebra: Dual Spaces, Dual Maps, and All That

An exploration of duality in linear algebra, including dual spaces, dual maps, and dual bases, with connections to linear and bilinear forms, adjoints in real and complex inner product spaces, covariance and contravariance, and matrix rank. More videos on linear algebra: https://youtube.c

From playlist Summer of Math Exposition Youtube Videos

Tetrahedral hyperbolic 3-manifolds and links by Andrei Vesnin

PROGRAM KNOTS THROUGH WEB (ONLINE) ORGANIZERS: Rama Mishra, Madeti Prabhakar, and Mahender Singh DATE & TIME: 24 August 2020 to 28 August 2020 VENUE: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conducted through onl

From playlist Knots Through Web (Online)

Biological Sciences M121. Immunology with Hematology. Lecture 04. Innate Immunity.

UCI BioSci M121: Immunology with Hematology (Fall 2013) Lec 04. Immunology with Hematology -- Innate Immunity -- View the complete course: http://ocw.uci.edu/courses/biosci_m121_immunology_with_hematology.html Instructor: David A. Fruman, Ph.D. License: Creative Commons CC-BY-SA Terms of

From playlist Biological Sciences M121: Immunology with Hematology

Alexandru Dimca: Betti numbers of hypersurfaces and defects of linear systems III

Abstract: Our approach is a generalization of Griffiths' results expressing the cohomology ofa smooth hypersurface V: f=0 in a projective space \mathbb{P}^n in terms of some graded pieces of the Jacobian algebra of f. We will start by recalling these classical results. Then we explain t

From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Antonin Guilloux: Slimness in the 3-sphere

Viewed as the boundary at infinity of the complex hyperbolic plane, the 3-sphere is equipped with a contact structure. The interplay between this contact structure and limit sets of subgroups of PU(2,1) has deep consequences on the properties of these subgroups. Some limit sets enjoy the p

From playlist Geometry

Educ 151. Lec 12. Language and Literacy: Understanding Syntax, Part II

UCI Education 151: Language and Literacy (Fall 2011) Lec 12. Language and Literacy: Understanding Syntax, Part II View the complete course: http://ocw.uci.edu/courses/education_151_language_and_literacy.html Instructor: Penelope Collins License: Creative Commons CC-BY-SA Terms of Use: ht

From playlist Education 151: Language and Literacy

Adjoints

Algebraic properties of the adjoint. Null space and range of the adjoint. The matrix of T* is the conjugate transpose of the matrix of T.

From playlist Linear Algebra Done Right

Factorization-based Sparse Solvers and Preconditions, Lecture 5

Xiaoye Sherry Li's (from Lawrence Berkeley National Laboratory) lecture number five on Factorization-based sparse solves and preconditioners

From playlist Gene Golub SIAM Summer School Videos

Combination Locks - Intro to Algorithms

This video is part of an online course, Intro to Algorithms. Check out the course here: https://www.udacity.com/course/cs215.

From playlist Introduction to Algorithms

Complement (complexity)

Related pages