
This is How You Use the Chain Rule in Calculus
This is How You Use the Chain Rule in Calculus
From playlist Random calculus problems:)

B25 Example problem solving for a Bernoulli equation
See how to solve a Bernoulli equation.
From playlist Differential Equations

Solution can be found at http://lem.ma/rR Part of Problems, Paradoxes, and Sophisms Series Please post your comments on Lemma rather than here.
From playlist Problems, Paradoxes, and Sophisms

Some worked solutions to example problems on the Chain Rule, Taylor Series, and Leibniz' Rule.
From playlist MATH2018 Engineering Mathematics 2D

C49 Example problem solving a system of linear DEs Part 1
Solving an example problem of a system of linear differential equations, where one of the equations is not homogeneous. It's a long problem, so this is only part 1.
From playlist Differential Equations

Newcomb's paradox | Famous Math Problems 7 | NJ Wildberger
Newcomb's paradox was first studied by American physicist William Newcomb, and popularized by articles by Robert Nozick and famously Martin Gardner in one of his 1974 Mathematical Games columns in Scientific American. The paradox involves notions of free will, determinism, choice, probabil
From playlist Famous Math Problems
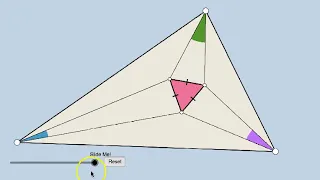
Morley's Theorem: Dynamic Illustration (w/o Words)
Link: https://www.geogebra.org/m/wwhDgwJd
From playlist Geometry: Challenge Problems

MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This class reviews Carpenter's Rule and properties of pseudotriangulation. Various proofs are presented, which cover topics includ
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

C19 Example problem using the superposition principle
Example problem using the superposition approach.
From playlist Differential Equations

Bazooka Charlie - WW2s Strangest Tank Buster
The extraordinary story of Major Charles Carpenter, known as "Bazooka Charlie", a Piper Cub spotter plane pilot who decided to turn his plane into a tank buster. Find out the full story here. Dr. Mark Felton is a well-known British historian, the author of 22 non-fiction books, including
From playlist Battle of Germany 1944-45

MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This lecture explores algorithms for unfolding 2D chains including ODE, pointed pseudotriangulations, and the energy method. Locki
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

Mocking can be a valuable tool in software testing, but mocking 3rd party libraries is nearly always a bad place to start. Dave Farley, author of books on Continuous Delivery and Software Engineering, demonstrates mocking 3rd party code with examples of code, tests and use of mocking, and
From playlist Automated Testing

When and How to Ask Programming Questions
Learn how to turn deep reinforcement learning papers into code: Get instant access to all my courses, including the new Prioritized Experience Replay course, with my subscription service. $24.99 a month gives you instant access to 35 hours of instructional content plus access to future up
From playlist Essential Soft Skills

Here I solve just one problem, but the level of difficulty of the problem was such that I was quite pleased to get it. The book reveals that it is due to John Conway, so I knew that there had to be a lower bound on its difficulty, and that there would almost certainly be some beautiful sur
From playlist Thinking about maths problems in real time: mostly invariants problems

Spoils of War for Britain and France - Redrawing the Map of the Middle East I THE GREAT WAR 1920
Sign up for Curiosity Stream and Nebula - and get 40% off annual plans right now: https://curiositystream.com/thegreatwar 100 years ago at the conference of San Remo, one thing became clear: Great Britain and France wanted control over the Middle East. Justified by the fighting in the pre
From playlist All Videos from THE GREAT WAR - chronological order

Lecture 12: Tensegrities & Carpenter's Rules
MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This lecture covers infinitesimal rigidity and motion, and tensegrity systems as an extension of rigidity theory. The rigidity mat
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

Husserl, Heidegger & Existentialism - Hubert Dreyfus & Bryan Magee (1987)
In this program, Hubert Dreyfus and Bryan Magee discuss the thinkers Husserl and Heidegger, as well as the movements of phenomenology and existentialism. Edmund Husserl was a 20th-century German philosopher, best known for founding phenomenology, a philosophical movement and methodology of
From playlist Bryan Magee Interviews - The Great Philosophers (1987)

Twelve Ways to Trisect an Angle – David Richeson
We all know that it is impossible to trisect an angle, right? It is impossible using only a compass and straightedge. But it is possible if we change the rules. For G4G12 we present a dozen ways to trisect an angle.
From playlist G4G12 Videos

How Do You Design a Just Society? | Thought Experiment: The Original Position
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateidea Thought Experiment: John Rawls’ Original Position We got merch! http://bit.ly/1U8fS1B Tweet us! http://bit.ly/pbsideachanneltwitter Idea Channel Facebook! http://bit.l
From playlist Newest Episodes

B15 Example problem with a linear equation using the error function
Solving an example problem for a linear equation with the error function.
From playlist Differential Equations