
Inner & Outer Semidirect Products Derivation - Group Theory
Semidirect products are a very important tool for studying groups because they allow us to break a group into smaller components using normal subgroups and complements! Here we describe a derivation for the idea of semidirect products and an explanation of how the map into the automorphism
From playlist Group Theory

Walter van Suijlekom: Semigroup of inner perturbations in Non Commutative Geometry
Starting with an algebra, we define a semigroup which extends the group of invertible elements in that algebra. As we will explain, this semigroup describes inner perturbations of noncommutative manifolds, and has applications to gauge theories in physics. We will present some elementary e
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

(ML 19.5) Positive semidefinite kernels (Covariance functions)
Definition of a positive semidefinite kernel, or covariance function. A simple example. Explanation of terminology: autocovariance, positive definite kernel, stationary kernel, isotropic kernel, covariogram, positive definite function.
From playlist Machine Learning
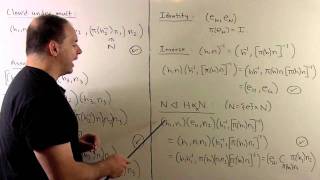
EDIT: At 6:24, the product should be "(e sub H, e sub N)", not "(e sub H, e sub G)" Abstract Algebra: Using automorphisms, we define the semidirect product of two groups. We prove the group property and construct various examples, including the dihedral groups. As an application, we
From playlist Abstract Algebra

Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

Joachim Cuntz: Semigroup C*-algebras and toric varieties
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. The coordinate ring of a toric variety is the semigroup ring of a finitely generated subsemigroup of Zn. Such semigroups have the interesting feature that their family of constructib
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Inner Semidirect Product Example: Dihedral Group
Semidirect products explanation: https://youtu.be/Pat5Qsmrdaw Semidirect products are very useful in group theory. To understand why, it's helpful to see an example. Here we show how to write the dihedral group D_2n as a semidirect product, and how we can describe that purely using cyclic
From playlist Group Theory

Abstract Algebra: We consider conditions for when a group is isomorphic to a direct or semidirect product. Examples include groups of order 45, 21, and cyclic groups Z/mn, where m,n are relatively prime. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-grou
From playlist Abstract Algebra

Categories 6 Monoidal categories
This lecture is part of an online course on categories. We define strict monoidal categories, and then show how to relax the definition by introducing coherence conditions to define (non-strict) monoidal categories. We finish by defining symmetric monoidal categories and showing how super
From playlist Categories for the idle mathematician

34 Sundar - Invariant measures and ergodicity for stochastic Navier-Stokes equations
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security

Dirk Blömker: Modulation Equations for SPDEs on unbounded domains
The lecture was held within the of the Hausdorff Junior Trimester Program: Randomness, PDEs and Nonlinear Fluctuations. Abstract: We consider the approximation via modulation equations for nonlinear stochastic partial differential equations (SPDEs) like the stochastic Swift-Hohenberg (SH)
From playlist HIM Lectures: Junior Trimester Program "Randomness, PDEs and Nonlinear Fluctuations"

Bernard Helffer: Spectral theory and semi-classical analysis for the complex Schrödinger operator
Abstract: We consider the operator Ah=−h2Δ+iV in the semi-classical limit h→0, where V is a smooth real potential with no critical points. We obtain both the left margin of the spectrum, as well as resolvent estimates on the left side of this margin. We extend here previous results obtaine
From playlist Mathematical Physics

57 Sundar - Invariant measures and ergodicity for stochastic Navier-Stokes equations
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Courses - A. Kupiainen “Quantum Field Theory for Probabilists”
The course consists of two parts. In the first one we give an introduction to the Renormalization Group as a method to study quantum field theory and statistical mechanics models at critical temperature. In the second part we apply these ideas to proving existence and uniqueness of solutio
From playlist T1-2015 : Disordered systems, random spatial processes and some applications

Control of fluid motion by Mythily Ramaswamy
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Concentration of quantum states from quantum functional (...) - N. Datta - Workshop 2 - CEB T3 2017
Nilanjana Datta / 24.10.17 Concentration of quantum states from quantum functional and transportation cost inequalities Quantum functional inequalities (e.g. the logarithmic Sobolev- and Poincaré inequalities) have found widespread application in the study of the behavior of primitive q
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

On the structure of quantum Markov semigroups - F. Fagnola - PRACQSYS 2018 - CEB T2 2018
Franco Fagnola (Department of Mathematics, Politecnico di Milano, Italy) / 06.07.2018 On the structure of quantum Markov semigroups We discuss the relationships between the decoherence-free subalgebra and the structure of the fixed point subalgebra of a quantum Markov semigroup on B(h) w
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

BAG1.4. Toric Varieties 4 - Spec(R) and Affine Semigroups
Basic Algebraic Geometry: In this part, we introduce Spec(R) and affine semigroups. This allows us to give yet another characterization of affine toric varieties in terms of affine semigroups.
From playlist Basic Algebraic Geometry

Definition of the Symmetric Group
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of the Symmetric Group
From playlist Abstract Algebra