
Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra
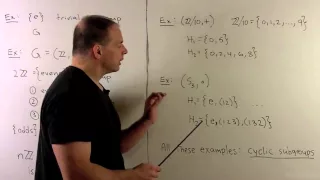
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Abstract Algebra: We introduce the notion of a group and describe basic properties. Examples given include familiar abelian groups and the symmetric groups. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-theory Master list at http://mathdoctorbob.o
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Group Theory: The Center of a Group G is a Subgroup of G Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof
From playlist Abstract Algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Arithmetic applications of automorphic forms - Andrew Wiles
Automorphic Forms Andrew Wiles Institute for Advanced Study April 7, 2001 Concepts, Techniques, Applications and Influence April 4, 2001 - April 7, 2001 Support for this conference was provided by the National Science Foundation Conference Page: https://www.math.ias.edu/conf-automorph
From playlist Mathematics

Limits of cubic differentials and projective structures by David Dumas
ORGANIZERS Siddhartha Gadgil, Krishnendu Gongopadhyay, Subhojoy Gupta and Mahan Mj DATE & TIME 27 November 2017 to 30 November 2017 VENUE Ramanujan Lecture Hall, ICTS Bangalore The focus of this discussion meeting will be geometric aspects of the representation spaces of surface groups int
From playlist Surface Group Representations and Geometric Structures

Andrea Bianchi (12/17/20): An upper bound on the topological complexity of discriminantal varieties
Title: An upper bound on the topological complexity of discriminantal varieties Abstract: A discriminantal variety V is the complement in C^m of the zero locus of a polynomial. Many interesting spaces arise in this way: for example both the ordered configuration space F_n(R^2) and the uno
From playlist Topological Complexity Seminar

On exceptional zero conjecture (Mazur-Tate-Teitelbaum) by Srilakshmi Krishnamoorthy
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Teena Gerhardt - 3/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Franc Forstnerič - Non singular holomorphic foliations on Stein manifolds (Part 3)
Non singular holomorphic foliations on Stein manifolds (Part 3)
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Anthony Henderson: Hilbert Schemes Lecture 2
SMRI Seminar Series: 'Hilbert Schemes' Lecture 2 H is smooth Anthony Henderson (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to PhD students interested in representat
From playlist SMRI Course: Hilbert Schemes

Joel Kamnitzer - Symplectic Resolutions, Coulomb Branches, and 3d Mirror Symmetry 1/5
In the 21st century, there has been a great interest in the study of symplectic resolutions, such as cotangent bundles of flag varieties, hypertoric varieties, quiver varieties, and affine Grassmannian slices. Mathematicians, especially Braden-Licata-Proudfoot-Webster, and physicists obser
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Organic Chemistry Mechanism Challenge 2
Need some organic chemistry practice? Here's a tricky mechanism to try! Try all of the organic chemistry practice problems: http://bit.ly/ProfDaveOCPP Organic Chemistry Tutorials: http://bit.ly/ProfDaveOrgChem EMAIL► ProfessorDaveExplains@gmail.com PATREON► http://patreon.com/ProfessorD
From playlist Organic Chemistry Practice Problems

Lagrangian Floer theory (Lecture – 02) by Sushmita Venugopalan
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

The General Linear Group, The Special Linear Group, The Group C^n with Componentwise Multiplication
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The General Linear Group, The Special Linear Group, The Group C^n with Componentwise Multiplication
From playlist Abstract Algebra