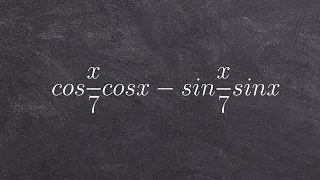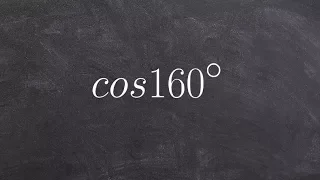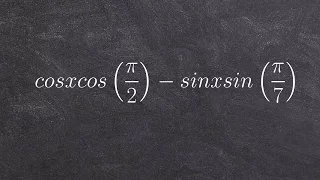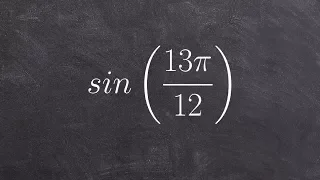Brahmagupta's interpolation formula
Brahmagupta's interpolation formula is a second-order polynomial interpolation formula developed by the Indian mathematician and astronomer Brahmagupta (598–668 CE) in the early 7th century CE. The Sanskrit couplet describing the formula can be found in the supplementary part of Khandakadyaka a work of Brahmagupta completed in 665 CE. The same couplet appears in Brahmagupta's earlier Dhyana-graha-adhikara, which was probably written "near the beginning of the second quarter of the 7th century CE, if not earlier." Brahmagupta was the one of the first to describe and use an interpolation formula using second-order differences. Brahmagupta's interpolation formula is equivalent to modern-day second-order Newton–Stirling interpolation formula. Mathematicians prior to Brahmagupta used a simple linear interpolation formula. The linear interpolation formula to compute f(a) is where . For the computation of f(a), Brahmagupta replaces Dr with another expression which gives more accurate values and which amounts to using a second-order interpolation formula. (Wikipedia).
