
Understanding Wealth Inequality
We've talked about public goods and externalities, and one negative externality associated with economic decisions is wealth inequality. A certain measure of wealth inequality is expected and desirable for any economy. But when this becomes extreme, as it is in the United States and many o
From playlist Economics
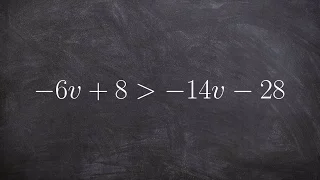
Solving and graphing a linear inequality
👉 Learn how to solve multi-step linear inequalities having no parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-ste
From playlist Solve and Graph Inequalities | Multi-Step Without Parenthesis

Solving and graphing an inequality
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Python - continued (part 1 of 3)
More coverage of the Python language. Part of a larger series on programming. Visit codeschool.org
From playlist Python - continued

Inequalities and more limits | Real numbers and limits Math Foundations 107 | N J Wildberger
The epsilon-delta definition of a limit of a sequence, going back to Cauchy and Weierstrass, is here dramatically simplified by restricting attention to the basic objects of calculus: rational polynumbers (or ``rational functions''). We review the basic definition and give a visual interpr
From playlist Math Foundations

*** This is CS50, Harvard University's introduction to the intellectual enterprises of computer science and the art of programming. *** HOW TO SUBSCRIBE http://www.youtube.com/subscription_center?add_user=cs50tv HOW TO TAKE CS50 edX: https://cs50.edx.org/ Harvard Extension School: ht
From playlist CS50 Shorts
Live CEOing Ep 174: Numerics in Wolfram Language
Watch Stephen Wolfram and teams of developers in a live, working, language design meeting. This episode is about Geometry in the Wolfram Language.
From playlist Behind the Scenes in Real-Life Software Design

Summary for solving and graphing compound inequalities
👉 Learn all about solving and graphing compound inequalities. An inequality is a statement in which one value is not equal to the other value. A compound inequality is a type of inequality comprising of more than one inequalities. To solve a compound inequality, we use inverse operations
From playlist Solve Compound Inequalities

Séminaire Bourbaki - 21/06/2014 - 3/4 - Thomas C. HALES
Developments in formal proofs A for mal proof is a proof that can be read and verified by computer, directly from the fundamental rules of logic and the foundational axioms of mathematics. The technology behind for mal proofs has been under development for decades and grew out of efforts i
From playlist Bourbaki - 21 juin 2014

Solving and graphing a multi-step inequality
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Samson Abramsky - The sheaf-theoretic structure of contextuality and non-locality
Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/AbramskySlidesToposesOnline.pdf Quantum mechanics implies a fundamentally non-classical picture of the physical worl
From playlist Toposes online
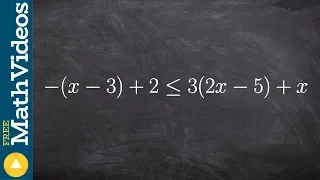
Solving and Graphing an inequality when the solution point is a decimal
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis
Regions in the complex plane | Linear Algebra MATH1141 | N J Wildberger
We show how the language of complex numbers and their polar forms allows us to describe certain regions of the complex plane. These are often given by inequalities involving either the modulus or argument of a complex number z. ************************ Screenshot PDFs for my videos are av
From playlist Higher Linear Algebra

Solving and graphing an inequality with infinite many solutions
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Acute and obtuse triangles | WildTrig: Intro to Rational Trigonometry | N J Wildberger
We define acute and obtuse triangles, and give inequalities for acuteness in terms of the spreads of the triangle. Then we look at the circumcenter of the triangle, and express it as an affine combination of the vertices. The Triangle spread rules play a role. This video is part of the Wi
From playlist WildTrig: Intro to Rational Trigonometry

Weighing with grams and ounces | Elementary Mathematics K-6 Explained 21 | N J Wildberger
We delve deeper into the measurement of weight, both in the metric system with grams, and in the Imperial system with ounces. There are 1000 grams in a kilogram, and there are 16 ounces in a pound. House hold items, specially those found in a kitchen, are often measured with grams and oun
From playlist Elementary Mathematics (K-6) Explained

Solving a multi step inequality with distributive property
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Solving a multi step inequality with distributive property
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

