
This talk is the first of two talks that give a proof of the Riemann Roch theorem, in the spacial case of nonsingular complex plane curves. We divide the Riemann-Roch theorem into 3 pieces: Riemann's theorem, a topological theorem identifying the three definitions of the genus, and Roch'
From playlist Algebraic geometry: extra topics

How to derive Euler's formula using differential equations! Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook A somewhat new proof for the famous formula of Euler. Here is the famous formula named after the mathematician Euler. It relates the exponential with cosin
From playlist Intro to Complex Numbers
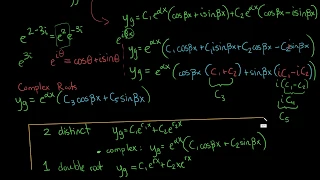
Differential Equations: Complex Roots of the Characteristic Equation
Homogeneous, constant-coefficient differential equations have a characteristic or auxiliary equation. The solution(s) of this equation yield the particular solutions to the homogeneous differential equation which, when combined, produce a general solution. In this video, we explore the cas
From playlist Differential Equations

I define one of the most important constants in mathematics, the Euler-Mascheroni constant. It intuitively measures how far off the harmonic series 1 + 1/2 + ... + 1/n is from ln(n). In this video, I show that the constant must exist. It is an open problem to figure out if the constant is
From playlist Series

Daichi Takeuchi - On local epsilon factors of the vanishing cycles of isolated singularities
The Hasse-Weil zeta function of a regular proper flat scheme over the integers is expected to extend meromorphically to the whole complex plane and satisfy a functional equation. The local epsilon factors of vanishing cycles are the local factors of the constant term in the functional equa
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

Complex Analysis (Advanced) -- This murderer inspired the results of my Ph.D. thesis
Excerpt from a talk I gave concerning my recent results on the Schwarz Lemma in Kähler and non-Kähler geometry. The talk details the classical Schwarz Lemma and discusses André Bloch. This is part 1 of a multi-part series. Part 1 -- https://youtu.be/AWqeIPMNhoA Part 2 -- https://youtu.be/
From playlist Complex Analysis

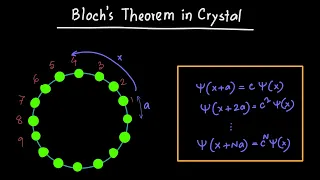
Bloch's Theorem and Fourier Series
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. There is a de
From playlist Electronics I: Semiconductor Physics and Devices

MIT 8.421 Atomic and Optical Physics I, Spring 2014 View the complete course: http://ocw.mit.edu/8-421S14 Instructor: Wolfgang Ketterle In this lecture, the professor reviewed Landau-Zener problem; discussed density matrix formalism for arbitrary two-level systems; and started the new cha
From playlist MIT 8.421 Atomic and Optical Physics I, Spring 2014

Towards low-complexity measurement-based feedback (...) - A. Sarlette - PRACQSYS 2018 - CEB T2 2018
Alain Sarlette (Department of Electronics and Information Systems, Ghent University, Belgium & QUANTIC lab, INRIA Paris, France) / 02.07.2018 Towards low-complexity measurement-based feedback control The control of quantum systems on the basis of continuous weak measurement has been deve
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

Informal Proof of Euler's Formula (2 of 2: Trigonometric calculus)
If you enjoyed this, you can also check out my expanded series of videos that introduces Euler's Formula from "first principles" and concludes with Euler's Identity: https://www.youtube.com/playlist?list=PLHZZ0otaqNsWV01h2ZssT17Tj8fbtLiuM More resources available at www.misterwootube.com
From playlist Introduction to Complex Numbers
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. In this video
From playlist Electronics I: Semiconductor Physics and Devices
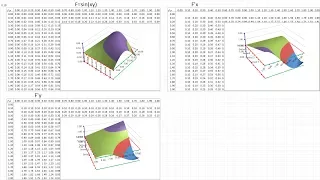
Properties of the derivatives of functions of several variables -- Calculus III
This lecture is on Calculus III. It follows Part III of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus III

Complex Numbers for ODEs (2 of 4)
ODEs: We describe basic properties of the complex numbers. A method for dividing complex numbers is given. Real and imaginary parts of a complex number are defined. Euler's formula is stated, and various consequences are interpreted.
From playlist Differential Equations

Cohomological decomposition of the diagonal in small dimension (Lecture - 05) by Claire Voisin
Infosys-ICTS Ramanujan Lectures Some new results on rationality Speaker: Claire Voisin (College de France) Date: 01 October 2018, 16:00 Venue: Madhava Lecture Hall, ICTS campus Resources Lecture 1: Some new results on rationality Date & Time: Monday, 1 October 2018, 04:00 PM Abstra
From playlist Infosys-ICTS Ramanujan Lectures

Recent Advances on Beilinson-Bloch-Kato Conjecture (Lecture 1) by Yifeng Liu
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Stefan Teufel: Peierls substitution for magnetic Bloch bands
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

Complex Numbers, Complex Variables, and Complex Functions
In this video we discuss complex numbers and show how they can be represented in various forms (rectangular or Euler’s formula) as well as how to perform basic operations on them. Topics and time stamps: 0:00 – Introduction 2:30 – Defining complex numbers in Matlab 11:00 – Math joke on co
From playlist Ordinary Differential Equations

In this video I derive the famous Cauchy-Riemann equations for a differentiable function of one complex variable. Those are equations that determine whether a complex function is differentiable or not, in terms of its real and imaginary parts. Zot zot :)
From playlist Complex Analysis

Stark-Heegner cycles for Bianchi modular forms by Guhan Venkat
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Masha Vlasenko: Gamma functions, monodromy and Apéry constants
Abstract: In 1978 Roger Apéry proved irrationality of zeta(3) approximating it by ratios of terms of two sequences of rational numbers both satisfying the same recurrence relation. His study of the growth of denominators in these sequences involved complicated explicit formulas for both vi
From playlist Algebraic and Complex Geometry