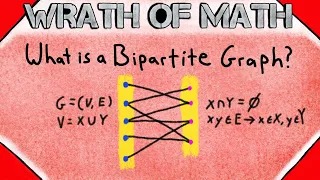
What is a Bipartite Graph? | Graph Theory
What is a bipartite graph? We go over it in today’s lesson! I find all of these different types of graphs very interesting, so I hope you will enjoy this lesson. A bipartite graph is any graph whose vertex set can be partitioned into two disjoint sets (called partite sets), such that all e
From playlist Graph Theory

What are Complete Bipartite Graphs? | Graph Theory, Bipartite Graphs
What are complete bipartite graphs? We'll define complete bipartite graphs and show some examples and non-examples in today's video graph theory lesson! Remember a graph G = (V, E) is bipartite if the vertex set V can be partitioned into two sets V1 and V2 (called partite sets) such that
From playlist Graph Theory

Bipartite Graphs with Isolated Vertices | Graph Theory, Complete Bipartite Graphs
We know what a bipartite graph is, and we know about complete bipartite graphs. But how do these definitions work with isolated vertices that have no neighbors? We'll go over just that in today's graph theory lesson! Remember that a bipartite graph is a graph whose vertices that can be pa
From playlist Graph Theory
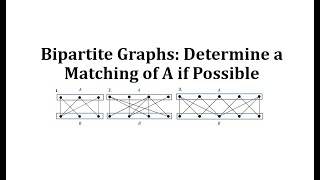
Bipartite Graphs: Determine a Matching of A if Possible
This video explains how to determine a matching of A in a bipartite and how to use Hall's Marriage theorem to explain why there I not a matching of A in a graph. mathispower4u.com
From playlist Graph Theory (Discrete Math)
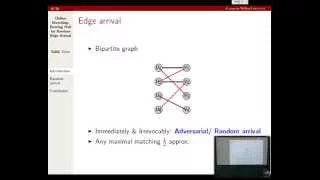
Sahil Singla: Online Matroid Intersection Beating Half for Random Arrival
We study a variant of the online bipartite matching problem that we call the online matroid intersection problem. For two matroids M1 and M2 defined on the same ground set E, the problem is to design an algorithm that constructs the largest common independent set in an online fashion. At e
From playlist HIM Lectures 2015

From playlist Graph Theory

Introduction to Matching in Bipartite Graphs (Hall's Marriage Theorem)
This video introduces matching in bipartite graphs. mathispower4u.com
From playlist Graph Theory (Discrete Math)

Discrete Math II - 10.2.2 Special Graphs: Bipartite Graphs
This video is a deeper look at bipartite graphs. We look at both the definition of a bipartite graph and using graph coloring to determine if an existing graph can be redrawn as bipartite. In addition, we model real-life scenarios with bipartite graphs in an effort to create a complete mat
From playlist Discrete Math II/Combinatorics (entire course)

MIT 6.042J Mathematics for Computer Science, Spring 2015 View the complete course: http://ocw.mit.edu/6-042JS15 Instructor: Albert R. Meyer License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.042J Mathematics for Computer Science, Spring 2015

OCR MEI MwA D: Graph Theory: 07 Bipartite Graphs
https://www.buymeacoffee.com/TLMaths Navigate all of my videos at https://sites.google.com/site/tlmaths314/ Like my Facebook Page: https://www.facebook.com/TLMaths-1943955188961592/ to keep updated Follow me on Instagram here: https://www.instagram.com/tlmaths/ Many, MANY thanks to Dea
From playlist OCR MEI MwA D: Graph Theory

Jørgen Bang-Jensen: Antistrong digraphs
Jørgen Bang-Jensen: Antistrong digraphs An antidirected trail in a digraph is a trail (a walk with no arc repeated) in which the arcs alternate between forward and backward arcs. An antidirected path is an antidirected trail where no vertex is repeated. We show that one can decide in line
From playlist HIM Lectures 2015

András Frank: Non TDI Optimization with Supermodular Functions
The notion of total dual integrality proved decisive in combinatorial optimization since it properly captured a phenomenon behind the tractability of weighted optimization problems. For example, we are able to solve not only the maximum cardinality matching (degree-constrained subdigraph,
From playlist HIM Lectures 2015

Anja Fischer: Polynomial Matroid Optimisation Problems
n this talk we consider polynomial matroid optimisation problems with some non-linear monomials in the objective function. The monomials are linearised and we study the corresponding polytopes. Extending results of Edmonds we present complete descriptions for the linearised polytopes for t
From playlist HIM Lectures: Trimester Program "Combinatorial Optimization"

Lauren Williams - Combinatorics of the amplituhedron
The amplituhedron is the image of the positive Grassmannian under a map in- duced by a totally positive matrix. It was introduced by Arkani-Hamed and Trnka to compute scattering amplitudes in N=4 super Yang Mills. I’ll give a gentle introduction to the amplituhedron, surveying its connecti
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

Kevin Hendrey - Obstructions to bounded branch-depth in matroids (CMSA Combinatorics Seminar)
Kevin Hendrey (Institute for Basic Science) presents “Obstructions to bounded branch-depth in matroids”, 24 November 2020 (CMSA Combinatorics Seminar).
From playlist CMSA Combinatorics Seminar

Joseph Bonin: Delta-matroids as subsystems of sequences of Higgs lifts
Abstract: Delta-matroids generalize matroids. In a delta-matroid, the counterparts of bases, which are called feasible sets, can have different sizes, but they satisfy a similar exchange property in which symmetric differences replace set differences. One way to get a delta-matroid is to t
From playlist Combinatorics

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Yusuke Kobayashi: A weighted linear matroid parity algorithm
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: The matroid parity (or matroid matching) problem, introduced as a common generalization of matching and matroid intersection problems, is so gener
From playlist Follow-Up-Workshop "Combinatorial Optimization"

OCR MEI MwA D: Graph Theory: 09 Complete Bipartite Graphs
https://www.buymeacoffee.com/TLMaths Navigate all of my videos at https://sites.google.com/site/tlmaths314/ Like my Facebook Page: https://www.facebook.com/TLMaths-1943955188961592/ to keep updated Follow me on Instagram here: https://www.instagram.com/tlmaths/ Many, MANY thanks to Dea
From playlist OCR MEI MwA D: Graph Theory

Victor Chepoi: Simple connectivity, local to global, and matroids
Victor Chepoi: Simple connectivity, local-to-global, and matroids A basis graph of a matroid M is the graph G(M) having the bases of M as the vertex-set and the pairs of bases differing by an elementary exchange as edges. Basis graphs of matroids have been characterized by S.B. Maurer, J.
From playlist HIM Lectures 2015