Bin packing problem

Optimization algorithms and methods | Bin packing | Strongly NP-complete problems

The bin packing problem is an optimization problem, in which items of different sizes must be packed into a finite number of bins or containers, each of a fixed given capacity, in a way that minimizes the number of bins used. The problem has many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media and technology mapping in FPGA semiconductor chip design. Computationally, the problem is NP-hard, and the corresponding decision problem - deciding if items can fit into a specified number of bins - is NP-complete. Despite its worst-case hardness, optimal solutions to very large instances of the problem can be produced with sophisticated algorithms. In addition, many approximation algorithms exist. For example, the first fit algorithm provides a fast but often non-optimal solution, involving placing each item into the first bin in which it will fit. It requires Θ(n log n) time, where n is the number of items to be packed. The algorithm can be made much more effective by first sorting the list of items into decreasing order (sometimes known as the first-fit decreasing algorithm), although this still does not guarantee an optimal solution, and for longer lists may increase the running time of the algorithm. It is known, however, that there always exists at least one ordering of items that allows first-fit to produce an optimal solution. There are many variations of this problem, such as 2D packing, linear packing, packing by weight, packing by cost, and so on. The bin packing problem can also be seen as a special case of the cutting stock problem. When the number of bins is restricted to 1 and each item is characterised by both a volume and a value, the problem of maximizing the value of items that can fit in the bin is known as the knapsack problem. A variant of bin packing that occurs in practice is when items can share space when packed into a bin. Specifically, a set of items could occupy less space when packed together than the sum of their individual sizes. This variant is known as VM packing since when virtual machines (VMs) are packed in a server, their total memory requirement could decrease due to pages shared by the VMs that need only be stored once. If items can share space in arbitrary ways, the bin packing problem is hard to even approximate. However, if the space sharing fits into a hierarchy, as is the case with memory sharing in virtual machines, the bin packing problem can be efficiently approximated. Another variant of bin packing of interest in practice is the so-called online bin packing. Here the items of different volume are supposed to arrive sequentially, and the decision maker has to decide whether to select and pack the currently observed item, or else to let it pass. Each decision is without recall. In contrast, offline bin packing allows rearranging the items in the hope of achieving a better packing once additional items arrive. This of course requires additional storage for holding the items to be rearranged. (Wikipedia).

Math for Liberal Studies - Lecture 1.8.1 The Bin-Packing Problem

This is the first video for Math for Liberal Studies Section 1.8: Bin Packing and Scheduling. In this lecture, I discuss the general idea behind the bin-packing problem and talk about several examples of how this problem can occur in the real world.

From playlist Math for Liberal Studies Lectures

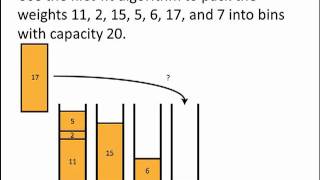
Math for Liberal Studies: Bin-Packing Algorithms

In this video, we use two different bin-packing algorithms to solve the same problem. For more info, visit the Math for Liberal Studies homepage: http://webspace.ship.edu/jehamb/mls/index.html

From playlist Math for Liberal Studies

OCR MEI MwA B: Bin Packing: 01 Introduction to Bin Packing

https://www.buymeacoffee.com/TLMaths Navigate all of my videos at https://sites.google.com/site/tlmaths314/ Like my Facebook Page: https://www.facebook.com/TLMaths-1943955188961592/ to keep updated Follow me on Instagram here: https://www.instagram.com/tlmaths/ Many, MANY thanks to Dea

From playlist OCR MEI MwA B: Bin Packing

Math for Liberal Studies - Lecture 1.8.2 One-at-a-Time Algorithms

This is the second video for Math for Liberal Studies Section 1.8: Bin Packing and Scheduling. In this lecture, I discuss two algorithms for solving bin-packing problems: the first-fit algorithm and the best-fit algorithm. I work through an example of each algorithm and discuss advantages

From playlist Math for Liberal Studies Lectures

Klaus Jansen: New Algorithmic Results for Bin Packing and Scheduling

From playlist Workshop: Parametrized complexity and discrete optimization

OCR MEI MwA B: Bin Packing: 07 Bin Packing Complexity

From playlist OCR MEI MwA B: Bin Packing

Math for Liberal Studies - Lecture 1.8.3 Sorted-Weight Algorithms

This is the third video for Math for Liberal Studies Section 1.8: Bin Packing and Scheduling. In this lecture, I discuss variations of the first-fit and best-fit packing algorithms. In these methods, we first sort the list of objects from largest to smallest before applying the packing alg

From playlist Math for Liberal Studies Lectures

Math for Liberal Studies - Lecture 1.8.4 Scheduling Problems

This is the last video for Math for Liberal Studies Section 1.8: Bin Packing and Scheduling. In this lecture, I discuss different types of scheduling problems and how we can apply bin-packing ideas to those problems. Specifically, I discuss the Longest-Processing-Time (LPT) algorithm and w

From playlist Math for Liberal Studies Lectures

Céline Swennenhuis: A Faster Exponential Time Algorithm for Bin Packing With Constant Bin Number

From playlist Workshop: Parametrized complexity and discrete optimization

Bin Packing Algorithms (Tutorial 5) D1 EDEXCEL A-Level

Powered by https://www.numerise.com/ This video is a tutorial on the Bin Packing Algorithms (First fit, first-fit decreasing, full-bin) for Decision 1 Math A-Level. Please make yourself revision notes while watching this and attempt my examples. Complete the suggested exercises from the

From playlist Decision 1: Edexcel A-Level Maths Full Course

Lecture 15 - Backtracking

This is Lecture 15 of the COMP300E (Programming Challenges) course taught by Professor Steven Skiena [http://www.cs.sunysb.edu/~skiena/] at Hong Kong University of Science and Technology in 2009. The lecture slides are available at: http://www.algorithm.cs.sunysb.edu/programmingchallenges

From playlist COMP300E - Programming Challenges - 2009 HKUST

Math for Liberal Studies: Longest Processing Time Algorithm

In this video, we use the Longest Processing Time algorithm to solve a scheduling problem. For more info, visit the Math for Liberal Studies homepage: http://webspace.ship.edu/jehamb/mls/index.html

From playlist Math for Liberal Studies

OCR MEI MwA B: Bin Packing: 05 Full-Bin Strategy Example

From playlist OCR MEI MwA B: Bin Packing

Bin packing problem

Related pages