From playlist Drawing a sphere
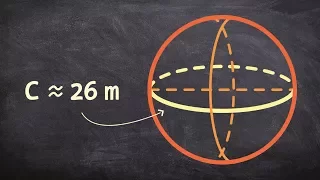
Find the volume of a sphere given the circumference
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

Finding the volume and the surface area of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area
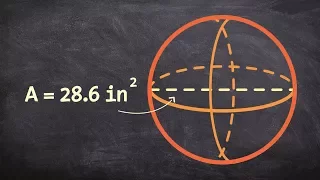
Learn how to determine the volume of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

How do you find the surface area of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

How do you find the volume of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

Data Science @Stanford- Bonnie Berger, PhD
Bonnie Berger, PhD, head of the Computational and Biology group at MIT's Computer Science and Artificial Intelligence Laboratory will discuss applying mathematical techniques to problems in molecular biology.
From playlist Data Science @ Stanford

Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - Barnabé Croizat - 17/11/17
En partenariat avec le séminaire d’histoire des mathématiques de l’IHP Ovales, cyclides et surfaces orthogonales : les premières amours géométriques de Darboux Barnabé Croizat, Laboratoire Paul Painlevé, Université Lille 1 & CNRS À l’occasion du centenaire de la mort de Gaston Darboux, l
From playlist Colloque d'histoire des sciences "Gaston Darboux (1842 - 1917)" - 17/11/2017

[BOURBAKI 2019]La démonstration de la conjecture de l'entropie positive d'Herman-Arnaud -16/10/2019
Marie-Claude Arnaud () / 16.11.2019 La démonstration de la conjecture de l'entropie positive d'Herman À l'ICM en 1998, Michel Herman énonce sa conjecture pour les difféomorphismes du disque qui préservent l'aire : dans tout voisinage de l'identité en topologie C∞, il existe un difféo
From playlist BOURBAKI - 2019

A Dyson Sphere is a megastructure that could be built around a star to harness all the solar energy it gives off. In this video we talk about the different kinds of Dyson Spheres, Dyson Clouds and other megastructures that could be built - and how we might even detect them from Earth. ht
From playlist Guide to Space

The art of asking the right questions | Tim Ferriss, Warren Berger, Hope Jahren & more | Big Think
The art of asking the right questions Watch the newest video from Big Think: https://bigth.ink/NewVideo Learn skills from the world's top minds at Big Think+: https://bigthink.com/plus/ ---------------------------------------------------------------------------------- Traditionally, intel
From playlist Ask the right questions | Big Think

Secularization and the Transformation of Faiths
Miroslav Volf, the Henry B. Wright Professor of Systematic Theology and Director for the Yale Center for Faith and Culture, explores the relationship between faiths and the forces of secularization.
From playlist Faith & Globalization 2009

More resources available at www.misterwootube.com
From playlist Measuring Further Shapes

Conversation Between Miroslav Volf & David Martin
Professor Miroslav Volf sits down with David Martin, Emeritus Professor of Sociology at the London School of Economics, to discuss the state of faiths in the world today and whether the "secularization thesis" is proving accurate.
From playlist Faith and Globalization

Rainbow fractional matchings - Ron Holzman
Computer Science/Discrete Mathematics Seminar I Topic: Rainbow fractional matchings Speaker: Ron Holzman Affiliation: Technion Date: December 2, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

D. Stern - Harmonic map methods in spectral geometry (version temporaire)
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to connections to the study of sphere-valued harmonic maps and minimal immersions. In this talk, I'll
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

D. Stern - Harmonic map methods in spectral geometry
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to connections to the study of sphere-valued harmonic maps and minimal immersions. In this talk, I'll
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Given the circumference how do you find the surface area of a hemisphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

AlgTop3: Two-dimensional surfaces: the sphere
After the plane, the two-dimensional sphere is the most important surface, and in this lecture we give a number of ways in which it appears. As a Euclidean sphere, we relate it to stereographic projection and the inversive plane. This is the third lecture in this beginner's course on Alge
From playlist Algebraic Topology: a beginner's course - N J Wildberger
