Trigonometry 6 The Sine of the Sum and the Difference of Two Angles
A description of the sine function of the sum and difference of two angles.
From playlist Trigonometry
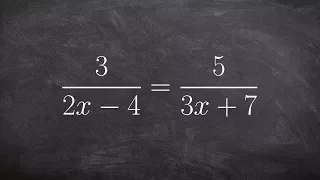
Learning the easy way to solve a a rational equation by using the LCD
π Learn how to solve proportions. Two ratios are said to be proportional when the two ratios are equal. Thus, proportion problems are problems involving the equality of two ratios. When given a proportion problem with an unknown, we usually cross-multiply the two ratios and then solve for
From playlist How to Solve Proportions with Trinomials
How to use the LCD to help us solve a rational equation
π Learn how to solve proportions. Two ratios are said to be proportional when the two ratios are equal. Thus, proportion problems are problems involving the equality of two ratios. When given a proportion problem with an unknown, we usually cross-multiply the two ratios and then solve for
From playlist How to Solve Rational Equations
Details of the triangle rasterization process. Not essential for the rest of the series. (revision of an earlier video: some restructuring and narration fixes)
From playlist OpenGL
Emilie Purvine (5/2/21): Homology of Graphs and Hypergraphs
Graphs and hypergraphs are typically studied from a combinatorial perspective. A graph being a collection of vertices and pairwise relationships (edges) among the vertices, and a hypergraph capturing multi-way or groupwise relationships (hyperedges) among the vertices. But both of these ob
From playlist TDA: Tutte Institute & Western University - 2021
Ch02n1: Barycentric forms of Lagrange polynomials
Barycentric forms of Lagrange polynomials. Numerical Computation, Chapter 2, additional video no 1. To be viewed after video ch2.2. Wen Shen, Penn State, 2018.
From playlist CMPSC/MATH 451 Videos. Wen Shen, Penn State University
Archimedes and the Law of the Lever Module 3: Vectors and Barycentric Co-ordinates
This is the third Module in the PD course (for high school maths educators) Mathematics in The Modern World: Archimedes and the Law of the Lever, which is available at https://www.openlearning.com/courses/archimedesthelawofthelever. In this Module, we look at Archimedes' Law of the Lever
From playlist Mathematics in The Modern World: PD courses for teachers
Jean-Yves Welschinger: Expected topology of a random subcomplex in a simplicial complex
Abstract: I will explain how to bound from above and below the expected Betti numbers of a random subcomplex in a simplicial complex and get asymptotic results under infinitely many barycentric subdivisions. This is a joint work with Nermin Salepci. It complements previous joint works with
From playlist Probability and Statistics
Affine Combinations and Barycentric Coords | Algebraic Calculus One | Wild Egg
In this video we show how affine combinations and barycentric coordinates express mathematically what Archimedes' Law of the Lever captures in terms of the centre of mass of a triangle. We examine both the one dimensional case of a segment, as well as the more general two dimensional case
From playlist Algebraic Calculus One from Wild Egg
8ECM Invited Lecture: Nick Trefethen
From playlist 8ECM Invited Lectures
Word Problems using trigonometry and bearings
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
Word Problems using trigonometry and bearings
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
WildLinAlg3: Center of mass and barycentric coordinates
Please watch: "UNSWTV: Entertaining your curiosity" https://www.youtube.com/watch?v=bQ7UO8nxiL0 -~-~~-~~~-~~-~- This video introduces several important applications of vectors. First we review the connections with force, velocity and acceleration, and introduce some games. Then we study
From playlist A first course in Linear Algebra - N J Wildberger
FEM@LLNL | Unifying the Analysis of Geometric Decomposition in FEEC
Sponsored by the MFEM project, the FEM@LLNL Seminar Series focuses on finite element research and applications talks of interest to the MFEM community. On March 22, 2022, Tobin Isaac of Georgia Tech presented "Unifying the Analysis of Geometric Decomposition in FEEC." Two operations take
From playlist FEM@LLNL Seminar Series
How to use trigonometry values to solve a word problem - Learn math online
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
Word Problems with trigonometry and triangles
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
Word Problems with trigonometry and triangles
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
Word Problems with trigonometry and triangles
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
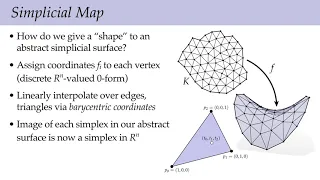
Lecture 14: Discrete Surfaces (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858
Word Problems with trigonometry and triangles
π Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions