Makoto Fujiwara: Bar theorem and bar recursion for continuous functions with continuous modulus
The lecture was held within the framework of the Hausdorff Trimester Program: Constructive Mathematics. Abstract: (joint work with Tatsuji Kawai) Bar induction is originally discussed by L. E. J. Brouwer under the name of “bar theorem” in his intuitionistic mathematics but first formali
From playlist Workshop: "Constructive Mathematics"

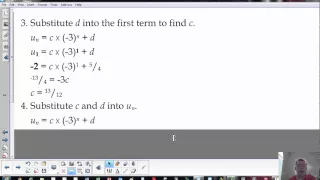
Applying the recursive formula to a sequence to determine the first five terms
👉 Learn all about recursive sequences. Recursive form is a way of expressing sequences apart from the explicit form. In the recursive form of defining sequences, each term of a sequence is expressed in terms of the preceding term unlike in the explicit form where each term is expressed in
From playlist Sequences
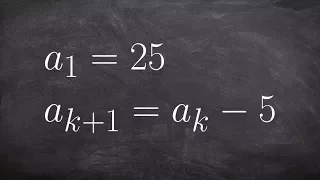
How to use the recursive formula to evaluate the first five terms
👉 Learn all about recursive sequences. Recursive form is a way of expressing sequences apart from the explicit form. In the recursive form of defining sequences, each term of a sequence is expressed in terms of the preceding term unlike in the explicit form where each term is expressed in
From playlist Sequences

Sequences: Introduction to Solving Recurrence Relations
This video introduces solving recurrence relations by the methods of inspection, telescoping, and characteristic root technique. mathispower4u.com
From playlist Sequences (Discrete Math)

How to determine the first five terms for a recursive sequence
👉 Learn all about recursive sequences. Recursive form is a way of expressing sequences apart from the explicit form. In the recursive form of defining sequences, each term of a sequence is expressed in terms of the preceding term unlike in the explicit form where each term is expressed in
From playlist Sequences

Using the recursive formula to find the first four terms of a sequence
👉 Learn all about recursive sequences. Recursive form is a way of expressing sequences apart from the explicit form. In the recursive form of defining sequences, each term of a sequence is expressed in terms of the preceding term unlike in the explicit form where each term is expressed in
From playlist Sequences

Get the Code: http://goo.gl/S8GBL Welcome to my Java Recursion tutorial. In this video, I'm going to cover java recursion in 5 different ways. I figured if I show it using many different diagrams that it will make complete sense. A recursive method is just a method that calls itself. As
From playlist Java Algorithms

Foundations - Seminar 14 - Gödel's incompleteness theorem Part 6
Billy Price and Will Troiani present a series of seminars on foundations of mathematics. In this seminar Will Troiani continues with the proof of Gödel's incompleteness theorem. You can join this seminar from anywhere, on any device, at https://www.metauni.org. This video was filmed in D
From playlist Foundations seminar

Bertrand Eynard - Considerations about Resurgence Properties of Topological Recursion
To a spectral curve $S$ (e.g. a plane curve with some extra structure), topological recursion associates a sequence of invariants: some numbers $F_g(S)$ and some $n$-forms $W_{g,n}(S)$. First we show that $F_g(S)$ grow at most factorially at large $g$, $F_g = O((
From playlist Resurgence in Mathematics and Physics

Yvain BRUNED - Bogoliubov Type Recursions for Renormalisation in Regularity Structures
Hairer's regularity structures transformed the solution theory of singular stochastic partial differential equations. The notions of positive and negative renormalisation are central and the intricate interplay between these two renormalisation procedures is captured through the combinatio
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Theory of Computation: A non-RE language
This video is for my Spring 2020 section of MA 342, for the class meeting on Wednesday April 22. Fast forward music is from "Now Get Busy" by the Beastie Boys, licensed Creative Commons Noncommercial Sampling Plus.
From playlist Math 342 (Theory of Computation) Spring 2020

Recursive combinatorial aspects of compactified moduli spaces – Lucia Caporaso – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.3 Recursive combinatorial aspects of compactified moduli spaces Lucia Caporaso Abstract: In recent years an interesting connection has been established between some moduli spaces of algebro-geometric objects (e.g. algebraic stable curves)
From playlist Algebraic & Complex Geometry

Applying the recursive formula to a geometric sequence
👉 Learn all about recursive sequences. Recursive form is a way of expressing sequences apart from the explicit form. In the recursive form of defining sequences, each term of a sequence is expressed in terms of the preceding term unlike in the explicit form where each term is expressed in
From playlist Sequences

From playlist CS50 Sections 2012

RubyConf 2016 - Rhythmic Recursion by Celeen Rusk
RubyConf 2016 - Rhythmic Recursion by Celeen Rusk One of the best things about multi-disciplinary work is recognizing familiar ideas in a different setting. It’s like running into an old friend while you’re on vacation halfway around the world-- “I had no idea you’d be here! It’s so great
From playlist RubyConf 2016

Elba Garcia-Failde - Quantisation of Spectral Curves of Arbitrary Rank and Genus via (...)
The topological recursion is a ubiquitous procedure that associates to some initial data called spectral curve, consisting of a Riemann surface and some extra data, a doubly indexed family of differentials on the curve, which often encode some enumerative geometric information, such as vol
From playlist Workshop on Quantum Geometry

TCO by: Chris Frisz Tail-call optimization (TCO) allows programmers to write interesting tail-recursive functions without worry of overflowing the program's stack memory. In languages that require constant space tail calls (i.e. Scheme and Standard ML), recursion becomes a natural and ef
From playlist Clojure Conf 2012