11_3_1 The Gradient of a Multivariable Function
Using the partial derivatives of a multivariable function to construct its gradient vector.
From playlist Advanced Calculus / Multivariable Calculus

👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Determining the scale factor of two quadrilaterals
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
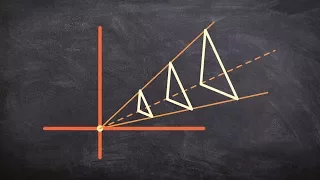
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

How to determine the reduction scale factor for two parallelograms
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
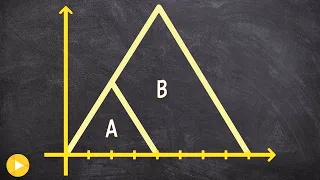
How to determine the scale factor of a dilation for enlargement
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
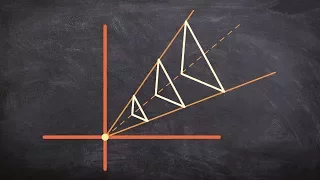
What are dilations, similarity and scale factors
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Álvaro Torras Casas (8/5/20): The Persistence Mayer-Vietoris spectral sequence
Title: The Persistence Mayer Vietoris spectral sequence Abstract: In this talk, I will give a brief introduction to the persistent Mayer-Vietoris spectral sequence. The original motivation for studying this object comes from the need to parallelize persistent homology computations. The st
From playlist AATRN 2020

What is an enlargement dilation
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Bradley Nelson (2/19/22): Parameterized Vietoris-Rips Filtrations via Covers
A challenge in computational topology is to deal with large filtered geometric complexes built from point cloud data such as Vietoris-Rips filtrations. This has led to the development of schemes for parallel computation and compression which restrict simplices to lie in open sets in a cove
From playlist Vietoris-Rips Seminar
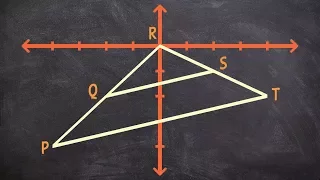
How to determine the scale factor for the dilation of two triangles
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
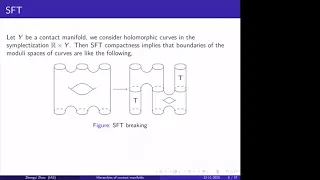
Hierarchies of contact manifolds via rational SFT - Zhengyi Zhou
IAS/PU-Montreal-Paris-Tel-Aviv Symplectic Geometry Topic: Hierarchies of contact manifolds via rational SFT Speaker: Zhengyi Zhou Affiliation: Member, School of Mathematics Date: December 11, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Richard Hain - 3/4 Universal mixed elliptic motives
Prof. Richard HAIN (Duke University, Durham, USA) Universal mixed elliptic motives are certain local systems over a modular curve that are endowed with additional structure, such as that of a variation of mixed Hodge structure. They form a tannakian category. The coordinate ring of its fu
From playlist Richard Hain - Universal mixed elliptic motives

Oussama Hamza - Hilbert series and mild groups
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):=sum_{n\in \NN} \dim_{\F_p} I^n(G)/I^{n+1}(G)$.The series $G(t)$ gives several information
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Jeremy Hahn : Prismatic and syntomic cohomology of ring spectra
CONFERENCE Recording during the thematic meeting : « Chromatic Homotopy, K-Theory and Functors» the January 24, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematicians on CIR
From playlist Topology

12_2_1 Taylor Polynomials of Multivariable Functions
Now we expand the creation of a Taylor Polynomial to multivariable functions.
From playlist Advanced Calculus / Multivariable Calculus

NEW TOPOLOGICAL LAYER in Graph Neural Networks (GCN), Filtrations, Persistent Homology - ICLR 2022
NEW: integrate a topological layer as one of the Graph Convolutional Network (GCN) layer in to your GCN to obtain essential topological info about the Graph. Persistent Homology, Learnable Filtrations and Topology. Topological Data Analysis (TDA). Although this method is limited to l=1, c
From playlist Learn Graph Neural Networks: code, examples and theory