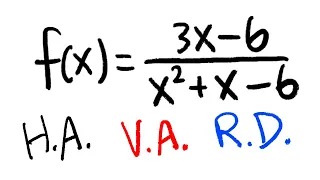Control theory | Signal processing
Asymptotic gain model
The asymptotic gain model (also known as the Rosenstark method) is a representation of the gain of negative feedback amplifiers given by the asymptotic gain relation: where is the return ratio with the input source disabled (equal to the negative of the loop gain in the case of a single-loop system composed of unilateral blocks), G∞ is the asymptotic gain and G0 is the direct transmission term. This form for the gain can provide intuitive insight into the circuit and often is easier to derive than a direct attack on the gain. Figure 1 shows a block diagram that leads to the asymptotic gain expression. The asymptotic gain relation also can be expressed as a signal flow graph. See Figure 2. The asymptotic gain model is a special case of the extra element theorem. As follows directly from limiting cases of the gain expression, the asymptotic gain G∞ is simply the gain of the system when the return ratio approaches infinity: while the direct transmission term G0 is the gain of the system when the return ratio is zero: (Wikipedia).