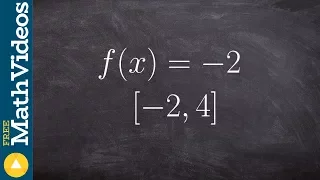
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Find the Interval That a Linear First Order Differential Equation Has a Unique Solution
This video explains how to determine the interval that a first order differential equation initial value problem would have a unique solution. Library: http://mathispower4u.com Search: http://mathispower4u.wordpress.com
From playlist Introduction to Differential Equations
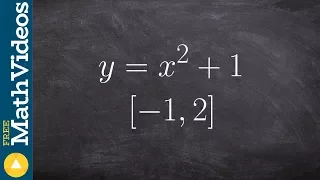
Find the max and min from a quadratic on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Determine the extrema of a function on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Proving an Equation has a Solution using the Intermediate Value Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proving an Equation has a Solution using the Intermediate Value Theorem
From playlist Calculus
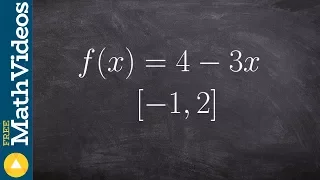
Find the max and min of a linear function on the closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
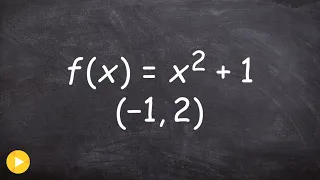
How to determine the absolute max min of a function on an open interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Find Values Excluded to Guarantee Existence and Uniqueness of Solution to a IVP - y'=f(t,y)
This video explains how to the values of a differential equation must be excluded to guarantee a unique solution exists. dy/dt=f(t,y) http://mathispower4u.com
From playlist Linear First Order Differential Equations: Interval of Validity (Existence and Uniqueness)
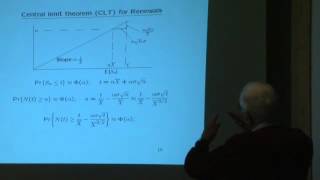
11. Renewals: Strong Law and Rewards
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

MA 15: Euler circuits and paths
This video is for my Spring 2020 section of MA 15, for the class meeting on Friday April 3. Fast forward music is from "Now Get Busy" by the Beastie Boys, licensed Creative Commons Noncommercial Sampling Plus.
From playlist Math 15 Spring 2020

MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Ex 1: Find the Interval that Guarantees a Solution to an IVP Exists (Interval of Validity)
This video explains how to find the interval that guarantees a a solution to a initial value problem involving a linear first order differential equation. http://mathispower4u.com
From playlist Linear First Order Differential Equations: Interval of Validity (Existence and Uniqueness)

13. Little, M/G/1, Ensemble Averages
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Heads-Tails and Heads-Heads are different? The ABRACADABRA Theorem for coin flips and dice #SoME2
Which takes more coin flips to come up on average, Heads-Tails or Heads-Heads? What about HHTT vs HTHT? Find out how long it takes and why using the magical ABRACADABRA Theorem. The method also works for dice rolls, the speeding rule in Monopoly, or a monkey typing at a typewriter. Video
From playlist Summer of Math Exposition 2 videos

S23.1 Poisson Versus Normal Approximations to the Binomial
MIT RES.6-012 Introduction to Probability, Spring 2018 View the complete course: https://ocw.mit.edu/RES-6-012S18 Instructor: John Tsitsiklis License: Creative Commons BY-NC-SA More information at https://ocw.mit.edu/terms More courses at https://ocw.mit.edu
From playlist MIT RES.6-012 Introduction to Probability, Spring 2018

Math Explorations Ep22, Euler circuits & paths (Mar 23, 2022)
This is a recording of a live class for Math 1015, Mathematics: An Exploration, an undergraduate course for non-technical majors at Fairfield University, Spring 2022. The major topics are voting, gerrymandering, and graph theory. Handouts and homework are at the class website. Class web
From playlist Math 1015 (Mathematical Explorations) Spring 2022

MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

12. Renewal Rewards, Stopping Trials, and Wald's Inequality
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Introduction to Discrete and Continuous Functions
This video defines and provides examples of discrete and continuous functions.
From playlist Introduction to Functions: Function Basics

20. Markov Processes and Random Walks
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011