
Some geometric mechanisms for Arnold diffusion - Rafael de la Llave
Emerging Topics Working Group Topic: Some geometric mechanisms for Arnold diffusion Speaker: Rafael de la Llave Affiliation: Georgia Tech Date: April 10, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Arnold diffusion for `complete' families of perturbations with... - Amadeu Delshams
Emerging Topics Working Group Topic: Arnold diffusion for `complete' families of perturbations with two or three independent harmonics Speaker: Amadeu Delshams Affiliation: UPC Date: April 9, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

A wave spreading from a vertical strip in the reduced non-oscillatory Edblom-Orban-Epstein model of reaction-diffusion, from equation 8.8 of Robin Engelhardt's master's thesis: http://www.robinengelhardt.info/speciale/ Generated by the open-source program: http://code.google.com/p/reac
From playlist Ready

Arnold Diffusion via Normally Hyperbolic Invariant Cylinders and...Method, Part I - Vadim Kaloshin
Vadim Kaloshin Pennsylvania State University; Member, School of Mathematics March 7, 2012 In 1964 Arnold constructed an example of instabilities for nearly integrable systems and conjectured that generically this phenomenon takes place. There has been big progress attacking this conjecture
From playlist Mathematics

Arnold Diffusion via Normally Hyperbolic Invariant Cylinders... Part II - Ke Zhang
Ke Zhang Institute for Advanced Study March 21, 2012 In 1964 Arnold constructed an example of instabilities for nearly integrable systems and conjectured that generically this phenomenon takes place. There has been big progress attacking this conjecture in the past decade. Jointly with Ke
From playlist Mathematics

Watch more videos on http://www.brightstorm.com/science/biology SUBSCRIBE FOR All OUR VIDEOS! https://www.youtube.com/subscription_center?add_user=brightstorm2 VISIT BRIGHTSTORM.com FOR TONS OF VIDEO TUTORIALS AND OTHER FEATURES! http://www.brightstorm.com/ LET'S CONNECT! Facebook ► htt
From playlist Biology
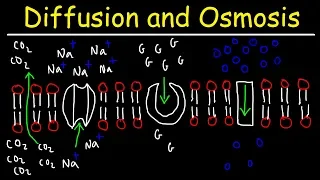
Diffusion and Osmosis - Passive and Active Transport With Facilitated Diffusion
This Biology video tutorial discusses diffusion and osmosis. It also mentions the difference between passive and active transport. Diffusion is the movement of any material down the concentration gradient. Osmosis is the diffusion of water. Facilitated diffusion is the movement of mate
From playlist Biology

Arnold Diffusion by Variational Methods - John Mather
John Mather Princeton University; Institute for Advanced Study October 26, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Arnold diffusion and Mather theory - Ke Zhang
Emerging Topics Working Group Topic: Arnold diffusion and Mather theory Speaker: Ke Zhang Affiliation: University of Toronto Date: April 11, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Some questions around quasi-periodic dynamics – Bassam Fayad & Raphaël Krikorian – ICM2018
Dynamical Systems and Ordinary Differential Equations Invited Lecture 9.2 Some questions around quasi-periodic dynamics Bassam Fayad & Raphaël Krikorian Abstract: We propose in these notes a list of some old and new questions related to quasi-periodic dynamics. A main aspect of quasi-per
From playlist Dynamical Systems and ODE
Arnold Diffusion by Variational Methods III - John Mather
John Mather Princeton University; Institute for Advanced Study November 9, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Jack Xin: "Lagrangian Approximations and Computations of Effective Diffusivities and Front Speed..."
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop IV: Stochastic Analysis Related to Hamilton-Jacobi PDEs "Lagrangian Approximations and Computations of Effective Diffusivities and Front Speeds in Chaotic and Stochastic Volume Preserving Flows" Jack Xin - University of California, Irvin
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Stability and Instability of Near-Integrable Hamiltonian Systems - Abed Bounemoura
Stability and Instability of Near-Integrable Hamiltonian Systems Abed Bounemoura Institute for Advanced Study September 20, 2011
From playlist Mathematics

Dynamical Glass by Sergej Flach
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Drugs, Dyes, & Mass Transfer: Crash Course Engineering #16
Today we’re talking about mass transfer. It doesn’t just apply to objects and fluids as a whole, but also to the individual molecules and components that make them up. We’ll see that transfers of mass need their own driving force, discuss diffusion, and use Fick’s Law to help us model mass
From playlist Engineering

A wave spreading from a gap in the reduced non-oscillatory Edblom-Orban-Epstein model of reaction-diffusion, from equation 8.8 of Robin Engelhardt's master's thesis: http://www.robinengelhardt.info/speciale/ Generated by the open-source program: http://code.google.com/p/reaction-diffus
From playlist Ready