
What are acute, obtuse, right, and straight angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

CCSS What is the difference between Acute, Obtuse, Right and Straight Angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
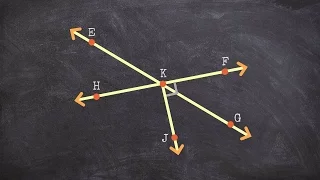
How to determine two acute adjacent angles from a figure
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What are adjacent angles and linear pairs
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What are examples of Vertical angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
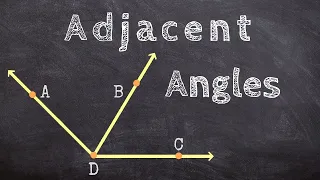
What are examples of adjacent angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Flat bands in twisted bilayer transition metal dichalcogenides by Manish Jain
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019

Topology, correlations and superconductivity in magic angle..(Lecture 2) by Ashvin Vishwanath
INFOSYS-ICTS CHANDRASEKHAR LECTURES ENTANGLEMENT AND TOPOLOGY IN QUANTUM SOLIDS SPEAKER: Ashvin Vishwanath (Harvard University) DATE: 23 December 2019, 16:00 to 17:00 VENUE: Ramanujan lecture hall, ICTS campus Lecture 1 : Entanglement and Topology in Quantum Solids. Date & Time : Mon
From playlist Infosys-ICTS Chandrasekhar Lectures

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Allan MacDonald: "Electronic and optical properties of 2D moiré superlattices"
Theory and Computation for 2D Materials "Electronic and optical properties of 2D moiré superlattices" Allan MacDonald Institute for Pure and Applied Mathematics, UCLA January 15, 2020 For more information: http://www.ipam.ucla.edu/tcm2020
From playlist Theory and Computation for 2D Materials 2020

MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This lecture focuses on the folding of the backbone chain of proteins in relation to fixed-angle linkages. Four problems types (sp
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

Rigidity of the hexagonal triangulation of the plane and its applications - Feng Luo
Feng Luo, Rutgers October 5, 2015 http://www.math.ias.edu/wgso3m/agenda 015-2016 Monday, October 5, 2015 - 08:00 to Friday, October 9, 2015 - 12:00 This workshop is part of the topical program "Geometric Structures on 3-Manifolds" which will take place during the 2015-2016 academic year
From playlist Workshop on Geometric Structures on 3-Manifolds

(January 28, 2013) Leonard Susskind presents three possible geometries of homogeneous space: flat, spherical, and hyperbolic, and develops the metric for these spatial geometries in spherical coordinates. Originally presented in the Stanford Continuing Studies Program. Stanford Universit
From playlist Lecture Collection | Cosmology

Lecture 3: Single-Vertex Crease Patterns
MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This lecture explores the local behavior of a crease pattern and characterizing flat-foldability of single-vertex crease patterns.
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

2020 Theory Winter School: Oskar Vafek
Topic: Topology and interactions in twisted bilayer graphene narrow bands For more information on the 2020 Theory Winter School: https://nationalmaglab.org/news-events/events/for-scientists/winter-theory-school
From playlist 2020 Theory Winter School

Determine the relationship between two angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Emergent geometric frustration and flat bands in twisted bilayer graphene by Hridis Kumar Pal
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019
