
Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra

Ring Theory: We define rings and give many examples. Items under consideration include commutativity and multiplicative inverses. Example include modular integers, square matrices, polynomial rings, quaternions, and adjoins of algebraic and transcendental numbers.
From playlist Abstract Algebra

Ideals in Ring Theory (Abstract Algebra)
An ideal of a ring is the similar to a normal subgroup of a group. Using an ideal, you can partition a ring into cosets, and these cosets form a new ring - a "factor ring." (Also called a "quotient ring.") After reviewing normal subgroups, we will show you *why* the definition of an ide
From playlist Abstract Algebra
The Normal Distribution (1 of 3: Introductory definition)
More resources available at www.misterwootube.com
From playlist The Normal Distribution

Confused about what a z-score is and how it relates to a bell curve? This short video explains in plain English what a z score is and what it's used for. Check out my Statistics Handbook: https://www.statisticshowto.com/the-practically-cheating-statistics-handbook/ Thanks for your support!
From playlist z-test

Units in a Ring (Abstract Algebra)
The units in a ring are those elements which have an inverse under multiplication. They form a group, and this “group of units” is very important in algebraic number theory. Using units you can also define the idea of an “associate” which lets you generalize the fundamental theorem of ar
From playlist Abstract Algebra
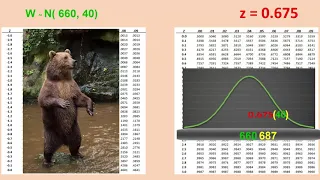
Determining values of a variable at a particular percentile in a normal distribution
From playlist Unit 2: Normal Distributions

Abstract Algebra | What is a ring?
We give the definition of a ring and present some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Relative p-Adic Hodge Theory - Ruochuan Liu
Ruochuan Liu Institute for Advanced Study December 2, 2010 The theory of φ,Γ)φ,Γ)-modules, which was introduced by Fontaine in the early 90's, classifies local Galois representations into modules over certain power series rings carrying certain extra structures (φandΓ)(φandΓ). In a recent
From playlist Mathematics

Toby Gee - 2/4 An Introduction to the Categorical p-adic Langlands (...)
An introduction to the ``categorical'' approach to the p-adic Langlands program, in both the ``Banach'' and ``analytic'' settings. Matthew Emerton (Chicago Univ.) Toby Gee (Imperial College) Eugen Hellman (Univ. Münster)
From playlist 2022 Summer School on the Langlands program

Introduction to the category of Adic spaces (Lecture 1) by Utsav Choudhury
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Felix Klein Lecture 2022 part6
From playlist Felix Klein Lectures 2022

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Commutative algebra 5 (Noetherian rings)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we find three equivalent ways of defining Noetherian rings, and give several examples of Noetherian and non-No
From playlist Commutative algebra

Perfectoid spaces (Lecture 4) by Kiran Kedlaya
PROGRAM PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France
From playlist Perfectoid Spaces 2019

Patricia Schmidt - Introduction to modelling gravitational waves from compact binaries
Recorded 21 September 2021. Patricia Schmidt of the University of Birmingham presents "Introduction to modelling gravitational waves from compact binaries" at IPAM's Mathematical and Computational Challenges in the Era of Gravitational Wave Astronomy Tutorial. Abstract: This tutorial will
From playlist Tutorials: Math & Computational Challenges in the Era of Gravitational Wave Astronomy

Normalized Table: Understand z scores, p values, critical values
Visual tutorial on normalized tables, z scores, p values, critical values. Related Video On Understanding Alpha, p values, z scores, critical values. http://youtu.be/zTABmVSAtT0 Like us on: http://www.facebook.com/PartyMoreStudyLess Professor of the Universe: David Longstreet http://w
From playlist Normalized Tables Z Scores Bell Curve Normal Table

Markus Rosenkranz Talk 1 7/8/14 Part 1
Title: A Noncommutative Mikusinski Calculus for Linear Boundary Problems
From playlist Spring 2014

