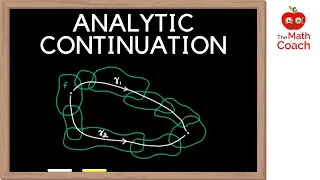
Analytic Continuation I The Identity Theorem I Complex Analysis #26
Analytic Continuation and the Identity theorem in Complex Analysis explained. Analytic continuation is a method to expand the domain of an analytic function and the Identity theorem tells us everything we need to know about analytic functions. The Identity Theorem is lowkey the greatest t
From playlist Summer of Math Exposition Youtube Videos

Math 135 Complex Analysis Lecture 07 021015: Analytic Functions
Definition of conformal mappings; analytic implies conformal; Cauchy-Riemann equations are satisfied by analytic functions; partial converses (some proven, some only stated); definition of harmonic functions; harmonic conjugates
From playlist Course 8: Complex Analysis

Analytic Geometry Over F_1 - Vladimir Berkovich
Vladimir Berkovich Weizmann Institute of Science March 10, 2011 I'll talk on work in progress on algebraic and analytic geometry over the field of one element F_1. This work originates in non-Archimedean analytic geometry as a result of a search for appropriate framework for so called skel
From playlist Mathematics
Analytic Number Theory with Sage - Kamalakshya Mehatab
Video taken from: http://ekalavya.imsc.res.in/node/451
From playlist Mathematics

Christian Bär - Boundary value problems for Dirac operators
This introduction to boundary value problems for Dirac operators will not focus on analytic technicalities but rather provide a working knowledge to anyone who wants to apply the theory, i.e. in the study of positive scalar curvature. We will systematically study "elliptic boundary conditi
From playlist Not Only Scalar Curvature Seminar

Paolo Piazza: Proper actions of Lie groups and numeric invariants of Dirac operators
HYBRID EVENT shall explain how to define and investigate primary and secondary invariants of G-invariant Dirac operators on a cocompact G-proper manifold, with G a connected real reductive Lie group. This involves cyclic cohomology and Ktheory. After treating the case of cyclic cocycles a
From playlist Lie Theory and Generalizations

The Schwarz Lemma -- Complex Analysis
Part 1 -- The Maximum Principle: https://youtu.be/T_Msrljdtm4 Part 3 -- Liouville's theorem: https://www.youtube.com/watch?v=fLnRDhhzWKQ In today's video, we want to take a look at the Schwarz lemma — this is a monumental result in the subject of one complex variable, and has lead to many
From playlist Complex Analysis

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

Omar Mohsen: Characterization of Maximally Hypoelliptic Differential Operators
Talk by Omar Mohsen in Global Noncommutative Geometry Seminar (Americas) on September 16, 2022, https://globalncgseminar.org/talks/talk-by-omar-mohsen/
From playlist Global Noncommutative Geometry Seminar (Americas)

In this *improvised* video, I rigorously prove some properties of the exponential function, namely that e^(x+y) = e^x e^y, e^-x = 1/e^x and e^ax = (e^x)^a The only assumption I'm using is that e^x is the unique solution of the differential equation y' = y with y(0) = 1 and y is positive 0
From playlist Differentiation

Chris WENDL - 3/3 Classical transversality methods in SFT
There are easy examples showing that classical transversality methods cannot always succeed for multiply covered holomorphic curves, but the situation is not hopeless. In this talk I will describe two approaches that sometimes lead to interesting results: (1) analytic perturbation theory,
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

J. Fine - Knots, minimal surfaces and J-holomorphic curves
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space which have ideal boundary equal to L, and in this way obtain a knot invariant. In other words the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

J. Fine - Knots, minimal surfaces and J-holomorphic curves (version temporaire)
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space which have ideal boundary equal to L, and in this way obtain a knot invariant. In other words the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Riemannian Exponential Map on the Group of Volume-Preserving Diffeomorphisms - Gerard Misiolek
Gerard Misiolek University of Notre Dame; Institute for Advanced Study October 19, 2011 In 1966 V. Arnold showed how solutions of the Euler equations of hydrodynamics can be viewed as geodesics in the group of volume-preserving diffeomorphisms. This provided a motivation to study the geome
From playlist Mathematics

7 juillet 2015
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Dimitri Zvonkine - On two ELSV formulas
The ELSV formula (discovered by Ekedahl, Lando, Shapiro and Vainshtein) is an equality between two numbers. The first one is a Hurwitz number that can be defined as the number of factorizations of a given permutation into transpositions. The second is the integral of a characteristic class
From playlist 4th Itzykson Colloquium - Moduli Spaces and Quantum Curves

Perturbation methods for nonlinear PDEs (Lecture - 01) by Vishal Vasan
ICTS Lecture by Vishal Vasan on 1, 3, 7, & 8th May, 2019 at 11:00 AM Title : Perturbation methods for nonlinear PDEs Speaker : Vishal Vasan, ICTS – TIFR, Bangalore Date : 01/05/2019 (Lecture 1) 03/05/2019 (Lectu
From playlist Seminar Series

