
Algebraic Expressions (Basics)
This video is about Algebraic Expressions
From playlist Algebraic Expressions and Properties

Yusuke Kobayashi: A weighted linear matroid parity algorithm
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: The matroid parity (or matroid matching) problem, introduced as a common generalization of matching and matroid intersection problems, is so gener
From playlist Follow-Up-Workshop "Combinatorial Optimization"

Quantum Geometry of Matroids by Dhruv Ranganathan
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS: Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

algebraic geometry 25 Morphisms of varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of a morphism of varieties and compares algebraic varieties with other types of locally ringed spaces.
From playlist Algebraic geometry I: Varieties

Max Wakefield, Research talk - 9 February 2015
Max Wakefield (United States Naval Academy) - Research talk http://www.crm.sns.it/course/4049/ We study a few different perspectives (combinatorics, geometry, and algebra) of a new polynomial attached to a matroid. First we define the polynomial combinatorially and compute it for certain
From playlist Algebraic topology, geometric and combinatorial group theory - 2015

An interesting homotopy (in fact, an ambient isotopy) of two surfaces.
From playlist Algebraic Topology

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Gyula Pap: Linear matroid matching in the oracle model
Gyula Pap: Linear matroid matching in the oracle model Linear matroid matching is understood as a special case of matroid matching when the matroid is given with a matrix representation. However, for certain examples of linear matroids, the matrix representation is not given, and actuall
From playlist HIM Lectures 2015

Maxima and Minima for Quadratic and Cubics | Algebraic Calculus One | Wild Egg
Tangents of algebraic curves are best defined purely algebraically, without recourse to limiting arguments! We apply our techniques for finding such tangents to derive some familiar results for quadratic and cubic polynomial functions and their maxima and minima. We compare also with the c
From playlist Algebraic Calculus One

Connecting tropical intersection theory with polytope algebra in types A and B by Alex Fink
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

MATLAB Basics: Get The Most Out of MATLAB
In this livestream, Heather Gorr and Elsie Eigerman will be walking through the fundamentals of programming with MATLAB. This isn’t just for beginners; we’ll show you the latest and greatest tips and tricks to help you get the most out of MATLAB. We’ll also walk-through core concepts for t
From playlist MATLAB and Simulink Livestreams

The log-concavity conjecture and the tropical Laplacian - June Huh
June Huh Princeton University; Veblen Fellow, School of Mathematics February 17, 2015 The log-concavity conjecture predicts that the coefficients of the chromatic (characteristic) polynomial of a matroid form a log-concave sequence. The known proof for realizable matroids uses algebraic g
From playlist Mathematics
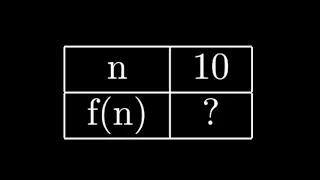
How Many Matroids of Size 10? - #MegaFavNumbers
A matroid is a generalisation of the idea of independence. How many matroids are there on 10 things? A video for #MegaFavNumbers. References: https://www.math.lsu.edu/~oxley/survey4.pdf https://oeis.org/A055545 https://bit.ly/3jzqIwt
From playlist MegaFavNumbers

Lauren Williams - Combinatorics of the amplituhedron
The amplituhedron is the image of the positive Grassmannian under a map in- duced by a totally positive matrix. It was introduced by Arkani-Hamed and Trnka to compute scattering amplitudes in N=4 super Yang Mills. I’ll give a gentle introduction to the amplituhedron, surveying its connecti
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

Algebraic and Convex Geometry of Sums of Squares on Varieties (Lecture 4) by Greg Blekherman
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS: Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is the study o
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

Galois theory: Transcendental extensions
This lecture is part of an online graduate course on Galois theory. We describe transcendental extension of fields and transcendence bases. As applications we classify algebraically closed fields and show hw to define the dimension of an algebraic variety.
From playlist Galois theory

Gary Gordon and Liz McMahon: Generalizations of Crapo's Beta Invariant
Abstract: Crapo's beta invariant was defined by Henry Crapo in the 1960s. For a matroid M, the invariant β(M) is the non-negative integer that is the coefficient of the x term of the Tutte polynomial. Crapo proved that β(M) is greater than 0 if and only if M is connected and M is not a loo
From playlist Combinatorics

Ilda Da Silva: How many cubes are orientable?
Abstract: A cube is a matroid over C^n={−1,+1}^n that contains as circuits the usual rectangles of the real affine cube packed in such a way that the usual facets and skew-facets are hyperplanes of the matroid. How many cubes are orientable? So far, only one: the oriented real affine cube
From playlist Combinatorics

James Oxley: A matroid extension result
Abstract: Let (A,B) be a 3-separation in a matroid M. If M is representable, then, in the underlying projective space, there is a line where the subspaces spanned by A and B meet, and M can be extended by adding elements from this line. In general, Geelen, Gerards, and Whittle proved that
From playlist Combinatorics