Novel Algebraic Operations for Affine Geometry | Algebraic Calculus One | Wild Egg
We introduce some novel conventions to help us set up the foundations of affine geometry. We learn about differences of points, sums of points and vectors, affine combinations and vector proportions. And then use these to state a number of important results from affine geometry, including
From playlist Algebraic Calculus One from Wild Egg

Affine and mod-affine varieties in arithmetic geometry. - Charles - Workshop 2 - CEB T2 2019
François Charles (Université Paris-Sud) / 24.06.2019 Affine and mod-affine varieties in arithmetic geometry. We will explain how studying arithmetic versions of affine schemes and their bira- tional modifications leads to a generalization to arbitrary schemes of both Fekete’s theorem on
From playlist 2019 - T2 - Reinventing rational points
Combinatorial affine sieve - Alireza Salehi Golsefidy
Speaker: Alireza Salehi Golsefidy (UCSD) Title: Combinatorial affine sieve Abstract: In this talk the general setting of affine sieve will be presented. Next I will explain the Bourgain-Gamburd-Sarnak method on proving affine sieve in the presence of certain spectral gap. Finally I will sa
From playlist Mathematics
Calculus and affine geometry of the magical parabola | Algebraic Calc and dCB curves 3 | Wild Egg
Algebraic Calculus naturally lives in affine geometry, not Euclidean geometry. Affine geometry is the geometry of parallelism, or (almost the same thing) --- the geometry of pure linear algebra. The parabola is characterized projectively in this geometry as the unique conic which is tangen
From playlist Algebraic Calculus One Info

How to encrypt and decrypt the affine cipher using Maple software. Code from Into to Crypto and Coding Theory 2nd ed. by W. Trappe and LC Washington.
From playlist Cryptography and Coding Theory

Chapter 3 - Laws of Exponents - IB Math Studies (Math SL)
Hello and welcome to What The Math. This is a Chapter 3 video about laws of exponents and exponent operations. This is a part of Chapter 3 from Harris Publication version of IB math book by Haese.
From playlist IB Math Studies Chapter 3

Abstract Algebra | Injective Functions
We give the definition of an injective function, an outline of proving that a given function is injective, and a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Simplify a rational expression by using properties of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule
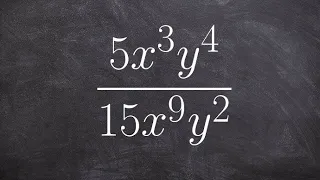
Simplify rational expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Affine Combinations and Barycentric Coords | Algebraic Calculus One | Wild Egg
In this video we show how affine combinations and barycentric coordinates express mathematically what Archimedes' Law of the Lever captures in terms of the centre of mass of a triangle. We examine both the one dimensional case of a segment, as well as the more general two dimensional case
From playlist Algebraic Calculus One from Wild Egg

Querying SQL Server 2012 Training Video | Logical Database Design Tutorial
www.simplilearn.com/os-and-databases/querying-microsoft-sql-server-2012-certification-training?utm_campaign=Logical-Database-Design-Rf9J_bTiMz4&utm_medium=SC&utm_source=youtube Logical Database Design The process of a database design there are two distinct phases and that's logical databas
From playlist Querying Microsoft SQL Server 2012 Tutorials

Quadrance, perpendicularity and pedal curves | Algebraic Calculus One | Wild Egg
We want to introduce metrical structure into our affine setting, allowing us to access Euclidean geometry and physical applications. To do this logically and carefully, with precise definitions, we want to take the view point of Rational Trigonometry: with quadrance and perpendicularity pl
From playlist Algebraic Calculus One from Wild Egg

Points and Lines in the Affine Plane | Algebraic Calculus One | Wild Egg
This is the first lecture in the Algebraic Calculus One course, which will present an exciting new approach to calculus, sticking with rational numbers and high school algebra. The course will be carefully framed on careful definitions, explicit examples and concrete computations. In thi
From playlist Algebraic Calculus One

Paul-André Melliès - A Functorial Excursion between Algebraic Geometry and Linear Logic
In this talk, I will use the functor of points approach to Algebraic Geometry to establish that every covariant presheaf X on the category of commutative rings — and in particular every scheme X — comes equipped “above it” with a symmetric monoidal closed category PshModX of presheaves of
From playlist Combinatorics and Arithmetic for Physics: special days

Marco Robalo - Motivic realisations of singularity categories and vanishing cycles
Abstract: In this talk I will explain a comparison result establishing an identification of the L-adic realisation of the dg-category of matrix factorisations of a Landau-Ginzburg model over a complete discrete valuation ring with potential induced by a uniformizer, with a 2-periodic versi
From playlist Algebraic Analysis in honor of Masaki Kashiwara's 70th birthday

Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 2
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Samuel Raskin: Spectral decomposition of the principal series category
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 4
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Sveta Makarova. Good moduli spaces for Artin stacks
Seminar talk on CORONA GS: https://murmuno.mit.edu/coronags Abstract: The talk is based on Alper's paper "Good moduli spaces for Artin stacks". I will briefly remind definitions of moduli problems and stacks and then proceed to explaining Alper's results. After that, I will focus on givin
From playlist CORONA GS

Affine Transformations — Topic 27 of Machine Learning Foundations
In this video we use hands-on code demos in NumPy to carry out affine transformations, a particular type of matrix transformation that may adjust angles or distances between vectors, but preserves parallelism. These operations can transform the target tensor in a variety of ways including
From playlist Linear Algebra for Machine Learning