
Dirichlet Eta Function - Integral Representation
Today, we use an integral to derive one of the integral representations for the Dirichlet eta function. This representation is very similar to the Riemann zeta function, which explains why their respective infinite series definition is quite similar (with the eta function being an alte rna
From playlist Integrals

What is an integral and it's parts
👉 Learn about integration. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower li
From playlist The Integral
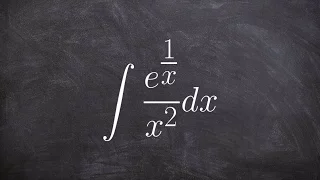
How to integrate exponential expression with u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Apply u substitution to a polynomial
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Integrate cosine using u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral
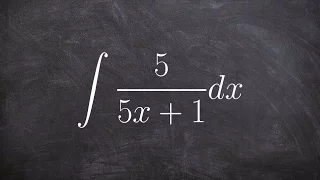
Integrate the a rational expression using logarithms and u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

How to find the integral of an exponential function using u sub
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral
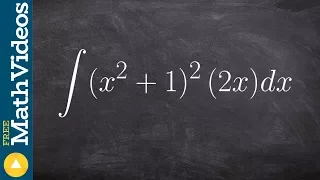
Apply u substitution with a binomial squared
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Introduction to elliptic curves and BSD Conjecture by Sujatha Ramadorai
12 December 2016 to 22 December 2016 VENUE Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution. An
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Jeffrey Achter, Equidistribution counts abelian varieties
VaNTAGe Seminar, February 22, 2022 License: CC-BY-NC-SA Links to some of the papers mentioned in this talk are listed below. Sutherland: https://arxiv.org/abs/1604.01256 Gekeler: https://academic.oup.com/imrn/article/2003/37/1999/863196 Job Rauch: https://www.universiteitleiden.nl/binar
From playlist Curves and abelian varieties over finite fields

Expanding a binomial to find the antiderivative
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

David Corwin, Kim's conjecture and effective Faltings
VaNTAGe seminar, on Nov 24, 2020 License: CC-BY-NC-SA.
From playlist ICERM/AGNTC workshop updates

Dynamical effects from topology in metals
Discussion Meeting: Quantum entanglement in macroscopic matter URL: http://www.icts.res.in/discussion_meeting/QEM2015/ Dates: Monday 12 Jan, 2015 - Friday 16 Jan, 2015 Description: Condensed matter systems display a wide variety of interesting low temperature phases that are the product
From playlist Discussion Meeting: Quantum entanglement in macroscopic matter

[BOURBAKI 2019] Manolescu’s work on the triangulation conjecture - Stipsicz - 15/06/19
András STIPSICZ Manolescu’s work on the triangulation conjecture The triangulation conjecture (asking whether a manifold is necessarily a simplicial complex) has been recently resolved in the negative by Ciprian Manolescu. His proof is based on work of Galweski–Stern and Matumoto, reduci
From playlist BOURBAKI - 2019

The Geometric Langlands conjecture and non-abelian Hodge theory (Lecture 3) by Ron Donagi
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Representation theory: Abelian groups
This lecture discusses the complex representations of finite abelian groups. We show that any group is iomorphic to its dual (the group of 1-dimensional representations, and isomorphic to its double dual in a canonical way (Pontryagin duality). We check the orthogonality relations for the
From playlist Representation theory

Akshay Venkatesh - 1/4 Analytic number theory around torsion homology
Akshay Venkatesh - Analytic number theory around torsion homology
From playlist École d'été 2014 - Théorie analytique des nombres

The Geometric Langlands conjecture and non-abelian Hodge theory (Lecture 1) by Ron Donagi
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Integrate using u sub with a binomial to a higher power
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

David Masser: Avoiding Jacobians
Abstract: It is classical that, for example, there is a simple abelian variety of dimension 4 which is not the jacobian of any curve of genus 4, and it is not hard to see that there is one defined over the field of all algebraic numbers \overline{\bf Q}. In 2012 Chai and Oort asked if ther
From playlist Algebraic and Complex Geometry